Spacetime, Special Relativity, and a Lot of Circles

(It's Glen again!)

This post is going to be long, and as the title suggests, contain very many circles. Relatedly, most of the diagrams in here are hand-drawn and scanned because no way am I going to figure out how draw all of these diagrams on computer. You have been warned.

0 Introduction

0.1 Working in 3D

I don't actually remember how I first thought of this. According to some self-stalking, the initial idea comes from a handout by David called "$\mathbb{RP}$_", but I can't seem to find this handout. Anyway, the idea is: given a circle of radius $r$ and centre $(a,b)$, we may view it instead as a point $(a,b,r)$ in $\mathbb R^3$. (In the spirit of things, I'm going to label circles as if they were points.)

An immediate application of this method is Monge's Theorem:

Theorem (Monge). Given three circles $X,Y,Z$ in the plane, their pairwise exsimilicentres are collinear.

(The exsimilicentre of two circles is their external centre of homothety, which you can construct by taking the intersection of their two external tangents, if they exist.)

Under our setup, the exsimilicentre of circles $X,Y$ is the intersection of $XY$ with the $xy$-plane:

So the line that all three exsimilicentres lie on is the intersection of the plane $XYZ$ with the $xy$-plane. $\square$

In fact, if we are willing to consider $(a,b,-r)$ for some circles instead, we can also find the insimilicentre:

The same idea as before (but with $Z$ below the $xy$-plane) lets us deduce

Theorem (d'Alembert). Given three circles $X,Y,Z$ in the plane, where $Z$ doesn't intersect $X,Y$, the exsimilicentre of $X,Y$ and the insimilicentres of $X,Z$ and $Y,Z$ are collinear.

This also tells us why we need there to be an even number of insimilicentres for these results to work. 

0.2 Working in spacetime

Having seen this trick, I thought "what a cool method!" and tried to apply it to other circle-y theorems. Eventually, the one I attempted to prove was Casey's theorem, which is a generalisation of Ptolemy's theorem:

Theorem (Casey). Let $\Gamma$ be a circle, and $A,B,C,D$ be circles tangent to $\Gamma$, with points of tangency arranged in that order. Then $d(A,B)d(C,D) + d(A,D)d(B,C) = d(A,C)d(B,D)$, where $d$ is the length of the external common tangent if both circles are externally tangent or both circles are internally tangent to $\Gamma$, and the length of the internal common tangent otherwise.

We see that if $A,B,C,D$ are points, we in fact get Ptolemy. Apparently, this is called a "blowup", because you're expanding points into circles or something.

What exactly is this distance $d(A,B)$? Well, if you look at the diagram below, it's $\sqrt{(\Delta x)^2 + (\Delta y)^2 - (\Delta r)^2}$.

If you're like me and were forced to learn special relativity because theoretical physics counts as math, this is extremely suspicious: this is the "distance" in the Minkowski metric! So it makes sense to view our $\mathbb R^3$ as a $(2+1)$-dimensional spacetime, with $r$ being the time direction.

If you don't know what any of that meant, don't worry; I'm going to explain it right now. We'll return to Casey's theorem later.

0.3 What is spacetime?

(Disclaimer: it's been a long time since I had to learn about special relativity so stuff might be slightly wonky.)

A fundamental idea underlying classical mechanics is that the laws of the physics are the same in every direction, at every point in space, at any time. This is why, when we do physics problems, we're allowed to resolve vectors onto any convenient set of orthogonal coordinates, or WLOG assume that $t=0$. You can think of different orientations/locations/times as different frames of reference, and the laws of physics are preserved by (orthonormal) changes of coordinates (i.e resolving vectors).

Special relativity says that the laws of physics and the speed of light are the same in all intertial frames, i.e. frames of reference which are moving at constant velocity. We're going to let the speed of light be $1$ for the sake of sanity (and to match our geometric picture). Suppose we have 1 spatial dimension, so we can describe our time and location by $(x,t)$ and that we're moving at a constant velocity $v$. We want to find a suitable change in coordinates $(x',t')$. Well, objects moving at constant velocity in one frame of reference are moving at constant velocity in the other (as Newton's laws of motion hold in both). These are lines in the $(x,t)$ plane, so $(x',t')$ and $(x,t)$ must be linearly related. Moreover, $x' $ must be of form $k(x-vt)$ so that our location is now constant in the new frame of reference. By the same reasoning, we have $x = k(x'+vt')$. Now apply the fact that the speed of light is $1$ in both, and a bit of bashing gives us $$x' = \frac1{\sqrt{1-v^2}} (x-vt), t' = \frac1{\sqrt{1-v^2}} (t-vx).$$

Such a change in coordinates is called a boost.

The same picture holds with more spatial dimensions (just add $y'=y$, etc.). We can go between all possible inertial frames by applying a combination of boosts, rotations in space, and translations in space and time. These are called Lorentz transformations. We're going to work with in (2+1)-dimensional (2 spatial, 1 temporal) spacetime from now on. A point $(x,y,t)$ in spacetime is an event.

Note that a corollary of the boost formula above is that objects can't travel at the speed of light. This means that any event in spacetime is only affected by/can only affect events which occur within this cone:

This is called the light cone of the event. Stuff outside the cone is space-like separated from the event: they are too far away. Stuff inside the cone is time-like separated, and stuff on the boundary is light-like separated.

Okay, that's enough physics for now. I'll talk about the Minkowski metric later.

0.4 How does this relate to what we're doing?

Compare the physics stuff we defined above to our geometrical setup.

Viewing $\mathbb R^3$ as spacetime, circles are now events, and the $xy$-plane is the present ($t=0$). Consider two circles, one in the future ($t>0$) and one in the past ($t<0$). Then they are disjoint if they're space-like separated and externally tangent iff they're light-like separated. Moreover, for two circles in the future, they're internally tangent iff they're light-like separated. So looking at things in this way lets us have a nice idea of tangent circles.

1 Lorentz transformations

While looking for geometry problems to apply special relativity to, I found this paper by Alexander Skutin. The relevant section is Section 8. For some reason, this paper only has a theorem statements and no proofs, and yet still somehow got accepted to arxiv. Anyway, here are proofs of a couple of his results which illustrate the power of special relativity.

1.1 The Miquel circle

Recall: in a complete quadrilateral, the four circles drawn below meet at a common point, the Miquel point.

Blowing some points up gives us the following generalisation:

Theorem. Consider quadrilateral $ABCD$, let $P = AB\cap CD, Q = AD\cap BC$. Consider circles $A',B',C',D'$ with centers $A,B,C,D$ and radii $r_A,r_B,r_C,r_D$ such that $\frac{PA}{PB} = \frac{r_A}{r_B}, \frac{PC}{PD} = \frac{r_C}{r_D}, \frac{QB}{QC} = \frac{r_B}{r_C}, \frac{QD}{QA} = \frac{r_D}{r_A}$. Consider the following four circles:

• The circle $\Omega_1$ through $P$ internally tangent to $B',C'$
• The circle $\Omega_2$ through $P$ internally tangent to $A',D'$
• The circle $\Omega_3$ through $Q$ internally tangent to $A',B'$
• The circle $\Omega_4$ through $Q$ internally tangent to $C',D'$

There's a circle that's tangent to all four circles.

This picture is slightly wrong, and we'll see why soon.

To avoid configuration issues, we're going to assume that $A',B',C',D'$ are reasonably small, so $P$ is not in their interior.

The first thing to notice is that the ratios just mean that $P,Q,A',B',C',D'$ are coplanar (taking all circles to be in the future). Let $\Pi$ be the plane through them.

At this point, you might be tempted to say "aha! $P,Q,A',B',C',D'$ form a complete quadrilateral, so just take its Miquel point and that's the circle we want". That's wrong. Let's think about this a little more carefully.

$P, B', C'$ are all circles which are (internally) tangent to $\Omega_1$, and so lie on its cone. They also lie on $\Pi$, which is a plane at an angle. So we know from whatever we learnt about conic sections in school that $\Pi \cap \Omega_1$ is an ellipse, which means that in all likelihood it doesn't actually go through the Miquel point of $P,Q,A',B',C',D'$.

But all hope is not lost! Note that the ellipses $\Pi \cap \Omega_i$, $i=1,2,3,4$ are all "pointed in the same way" (they have the same eccentricity and their semimajor axes are parallel), so we can apply a linear transformation to turn them all into circles, and then take the Miquel point of these four circles, which, upon reversing the transformation, is indeed the "Miquel circle" we wanted. $\square$

But wait!

If you know about special relativity, there's a chance you might have gone "hmm, that looks like length contraction", and you would be right! Notice that our plane $\Pi$ is at an angle of $<\frac{\pi}4$, and so is the "present" in an inertial frame! So instead, we could have just performed a Lorentz transformation to view $\Pi$ as the new present. Then, note that lines get sent to lines (Lorentz transformations are linear), and light cones get sent to light cones (Lorentz transformations preserve the speed of light), so our ellipses are now the intersections of light cones with the present, i.e. regular circles. So if you think about it, we're now left with proving...exactly the usual Miquel point. Tada!

Note that the length conditions were stricter than necessary: we could in fact have blown $P,Q$ up as well, as long as the resultant $A',B',C',D',P',Q'$ ended up be coplanar (and on an inertial frame).

Earlier, I said the diagram was slightly wrong. Why is this so? Well, the Miquel point $M$ is either internally tangent to all $\Omega_i$ (if it lies in the future) or externally tangent to all of them (if it lies in the past); we can't have a mix of both, which the diagram shows. So...yeah. Drawing circles is hard.

1.2 Pascal, but with 8 circles

Consider the following generalisation of Pascal's theorem:

Theorem. Let $X,Y$ be circles with $Y$ contained in $X$. Let $A,B,C,D,E,F$ be circles externally tangent to $Y$ and internally tangent to $X$. Define $P_{AB,DE}$ as follows: look at the convex quadrilateral $\mathcal Q_{AB,DE}$ formed by the external common tangents to $A,B$ and the external common tangents to $D,E$ and take the intersection of their diagonals. Define $P_{BC,EF},P_{CD,FA}$ similarly. Then these three points are collinear.

When $X=Y$, we have the regular version of Pascal's theorem.

Put $X$ in the future and $Y$ in the past, then $A,B,C,D,E,F$ lie on the intersection of their cones (and are in the future).

This intersection is in fact an ellipse: the easiest way to see this is to write the equations of both cones in the usual Cartesian coordinates and take the difference to get the equation of a plane. In particular, $A,B,C,D,E,F$ are coplanar, and lie on an inertial frame of reference (a plane that's "too steep" would intersect a light cone at a hyperbola, but just from looking at the picture the intersection has to be connected).

So as $A,B,C,D,E,F$ lie on an ellipse, Pascal's theorem for conics tells us that $AB\cap DE, BC\cap EF, CD \cap FA$ are collinear. However, this doesn't really help us with the $P_{\text{blah}}$.

Instead, we could perform a Lorentz transformation, so WLOG $A,B,C,D,E,F$ lie on a circle in the present. (If you want the specific transformation, it corresponds to the boost resulting from travelling from $Y$ to $X$ at constant velocity.) What used to be the present is now some other inertial plane $\Pi$, i.e. a plane at an angle. In our original diagram, $AB$ is coplanar with either of the external common tangents to $A,B$, since both pass through the exsimilicentre. These form the two "common tangent planes" to the light cones of $A$ and $B$. After applying the Lorentz transformation, these become the two common tangent planes to the light cones of $A,B$, which are exactly the two planes through $AB$ which meet the present plane at an angle of $\frac{\pi}4$.

What do these planes represent? If you think about it, this is exactly the locus of points (well, circles) which are tangent to the line $AB$; each plane represents the circles tangent to one side of $AB$. So the vertices of the quadrilateral $\mathcal Q_{AB,DE}$ are in fact now circles tangent to $AB,DE$, like in the following diagram:

But from regular Euclidean geometry, we know that the lines through opposite centres pass through $AB \cap DE$; in other words, $P_{AB,DE}$ now lies directly above $AB \cap DE$! So we're done: consider the vertical plane which we get by taking the line through $AB\cap DE, BC\cap EF, CD \cap FA$ and extending it upwards, then this intersects $\Pi$ on a line which contains all the $P_{\text{blah}}$. $\square$

1.3 Meta-commentary

When we do Euclidean geometry, several common tools we use are transformations of the plane: homotheties, spiral similarities, inversions. But why are these useful? If you think about it, we're implicitly using the fact that these geometric transformations preserve certain properties of the plane: homotheties preserve pretty much everything except for size; same for spiral similarities (except that instead of preserving lines' gradients absolutely, these instead preserve their gradients relative to each other). Both of these send lines to lines, circles to circles.

Inversion is a bit more interesting: it sends generalised circles (i.e. circles + lines) to generalised circles, and preserves angles of intersection (in particular, tangency). For anyone who's first learnt inversion, it's a magical technique that transforms circles (cannot bash, scary) into lines (can bash, less scary).

Lorentz transformations are a geometric transformation on spacetime. They send planes to planes and lines to lines. More interestingly, they send generalised circles (events in spacetime, i.e. points and circles; note this is different from inversion) to generalised circles, and light cones to light cones (and so preserve tangency relations). The arguments above are simply exploiting this fact, much in the same way that inversion simplifies a diagram.

But in fact, Lorentz transformations preserve something even more concrete: the Minkowski inner product.

2 Minkowski inner product

2.1 More physics

Let's think about rotations in regular Euclidean 2D (or 3D) space. These are linear maps which preserve lengths and angles (in fact, preserving lengths implies preserving angles, e.g. by taking cosine rule). We call these isometries of Euclidean space. If you let $(\cdot,\cdot)$ be the regular inner product, this is equivalent to saying rotations preserve the inner product, i.e. for all vectors $\mathbf{v},\mathbf{w}$ and rotations $R$, we have $(R\mathbf{v},R\mathbf{w}) = (\mathbf{v},\mathbf{w})$.

The fact that these rotations preserve the laws of physics underpins the laws of classical mechanics. Analogously, since Lorentz transformations underpin the laws of special relativity, we would expect something similar to hold.

This is in fact true: define the Minkowski inner product to be $((x,y,t),(x',y',t')) = xx' + yy' - tt'$. Then we can check that all Lorentz transformations preserve this (it's clear for spatial rotations, and as for boosts, you just do a bit of bashing).

Caveat: this is technically not an inner product per se; inner products have to be positive definite, i.e. $(\mathbf{v},\mathbf{v}) \ge 0$, with equality iff $\mathbf{v} = 0$. This is obviously not the case here, so the correct term to use would be something like "symmetric bilinear form", but as we constructed this as a counterpart to the regular inner product, this is the terminology we use.

Another caveat: some people have the opposite sign convention. I'm using this because it matches our setup from earlier.

Anyway, this new inner product is linear in both variables, and so can generally be used in the same way as the regular inner product, bearing in mind the caveat above.

The Euclidean inner product recovers the (Pythagorean) distance between points: in Euclidean space, $||\mathbf{x}-\mathbf{y}||^2 = (\mathbf{x}-\mathbf{y},\mathbf{x}-\mathbf{y})$.

Analogously, we could construct the Minkowski metric: let $||\mathbf{x}-\mathbf{y}||^2 = (\mathbf{x}-\mathbf{y},\mathbf{x}-\mathbf{y})$ where the RHS uses the Minkowski inner product.

(Yes, I know this isn't exactly well-defined, because you are taking square roots of negative numbers and stuff.)

This gives us an algebraic description of time/space/light-like separation: $\mathbf{x},\mathbf{y}$ are space-like separated if $(\mathbf{x}-\mathbf{y},\mathbf{x}-\mathbf{y})>0$, time-like if $<0$, and light-like if $=0$.

The important part is the last part, since we know that light-like separation is the same thing as tangency as circles.

2.2 Casey's theorem

Let's look at the statement again.

Theorem (Casey). Let $\Gamma$ be a circle, and $A,B,C,D$ be circles tangent to $\Gamma$, with points of tangency arranged in that order. Then $d(A,B)d(C,D) + d(A,D)d(B,C) = d(A,C)d(B,D)$, where $d$ is the length of the external common tangent if both circles are externally tangent or both circles are internally tangent to $\Gamma$, and the length of the internal common tangent otherwise.

Let each of $A,B,C,D$ be in the future or the past respectively depending on whether they're inside or outside $\Gamma$. By our arguments above, we may write $d(A,B) = \sqrt{(A-B,A-B)}$. (If we can draw the common tangent, then the circles are space-like separated.)

Now, note that all of $A,B,C,D$ lie on the light cone of $\Gamma$, and translation preserves the Minkowski inner product, so we may WLOG translate the diagram so that $\Gamma$ lands on the origin.

In this case, we have $$(A-B,A-B) = (A,A) + (B,B) - 2(A,B) = 0 + 0 - 2(A,B) = -2(A,B),$$ as $A,B$ are light-like separated from the origin.

We are left with proving $$\sqrt{(A,B)(C,D)} + \sqrt{(A,D)(B,C)} = \sqrt{(A,C)(B,D)}.$$

Now we use the linearity of the inner product: note that scaling $A$ by a factor scales both sides of the equation by the square root of that factor, so we may WLOG assume $A$ lies on the plane $t=1$. Likewise, we can do the same for $B,C,D$.

Reverse the algebra, and suddenly, we're just left with showing Ptolemy. $\square$

A sharp-eyed observer might notice that there is something slightly wrong with our statement of Casey: it's possible to get the following edge case with no common tangents!

But where regular Euclidean geometry fails, special relativity saves the day: we can instead define $d(A,B) = \sqrt{(A-B,A-B)}$ for some choice of square root, and Casey's theorem still holds by the arguments above.

2.3 Some more applications

I sent this proof to David when I first came up with it some years ago and he replied with some other cool results.

First, an exercise:

Lemma. Let $X,Y$ be circles, $Y$ contained in $X$. Let $A$ be a circle internally tangent to $X$ at $P$ and externally tangent to $Y$ at $Q$. Then as $A$ varies, $PQ$ passes through a fixed point.

(Hint: d'Alembert)

Similar to the blown-up version of Pascal's theorem, we have:

Theorem (Laguerre). $X,Y$ as above. Let $A,B,C$ be circles internally tangent to $X$ and externally tangent to $Y$. Moreover, assume that the tangency points of $B$ and the tangency points of $C$ are collinear. Then $d(A,B)^2 + d(A,C)^2 = d(B,C)^2$.

Perform a Lorentz transformation as in the blowup of Pascal's, then $X,Y$ are set to reflections of each other across the present, so as lines are sent to lines, $Z$ is sent to the centre of $(ABC)$. As the Lorentz transformation preserves Minkowski inner products, we're left with showing Thales' theorem. $\square$

Results in the same vein include:

(Try to prove these!)

2.4 Converse of Casey's theorem

For anyone who bashes, the converse of Casey's theorem is perhaps the most useful way to show that circles are tangent. Everyone says it's true. But why? (I spent quite a lot of time in my Olympiad days looking for a proof but to no avail.) I think a full converse would be slightly cursed for reasons I'll explain below, but I have a reasonable version. I'm afraid I don't have a super satisfying proof of it, but it is nonetheless still a proof, which I'm recording for posterity.

Theorem (Casey, converse). Let $A,B,C,D$ be circles in spacetime such that $A,B,C$ lie on a common light cone and $\sqrt{(A-B,A-B)(C-D,C-D)} + \sqrt{(A-D,A-D)(B-C,B-C)} = \sqrt{(A-C,A-C)(B-D,B-D)}$ for some choice in signs. Then $A,B,C,D$ lie on a common light cone.

Note that the final conclusion is stronger than saying that $A,B,C,D$ have a common tangent circle, because by fixing the orientation of the light cone, we are also determining whether the tangencies are internal or external (e.g. if $A,B$ are both in the future, then the tangent circle must be internally tangent to both or externally tangent to both.)

First, we show that $A,B,C$ in fact lie on the intersection of two light cones: consider the plane through them. If it's an inertial frame, perform a Lorentz transformation to make it the present, then $A,B,C$ lie on $(ABC)$ (which we can take to be in the present or in the past).

If the plane makes an angle of $>\frac{\pi}4$ with the present, we can perform a Lorentz transformation to make it a vertical plane. Then, as $A,B,C$ still lie on a common light cone (Lorentz transformations preserve light cones), so reflect it across the plane to get the second light cone. These are the two light cones that $D$ could possibly lie on.

Now fix the spatial location of $D$ and vary its time (radius) $r$. As $D$ varies, it intersects the two light cones at four points, which all satisfy the equation (for some choice of signs), by the regular direction of Casey. On the other hand, clearing the square roots by squaring both sides, moving the square root to one side and squaring again gives us a quartic in $r$, so there are at most four solutions, which are the four we've already found. $\square$

A note on the extra condition: recall that four collinear points satisfy the converse of Ptolemy, and similarly four collinear events (circles) would satisfy the equation. This is generally fine: if the line represents a trajectory with velocity $<1$, then all four circles share a common tangent line; if the line represents a light ray, then they're in fact all tangent at the same point. But funny things start happening if the light ray gets too vertical. You could have four circles with a common (interior) insimilicentre:

(If the line is vertical, we have four concentric circles.)

Morally, these still have a "common tangent line"; it just has like imaginary gradient or something. But we could take the example with four vertically-aligned points and perturb the top two a little, so no three lie on a common light cone but the equation is still satisfied. We'd expect there to be some "imaginary common tangent circle", but what is it?

So that's why I've added in that condition. Any case that we actually care about (e.g. when we can draw all the relevant internal/external tangents) satisfies the condition, so there really isn't much to worry about.

3 An actual application

3.1 An ISL problem

So far, we've just been using special relativity to prove weird versions of famous theorems. But in fact, it's not completely useless: there is a real-life Olympiad problem you could apply this to!

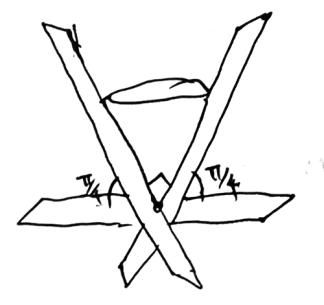
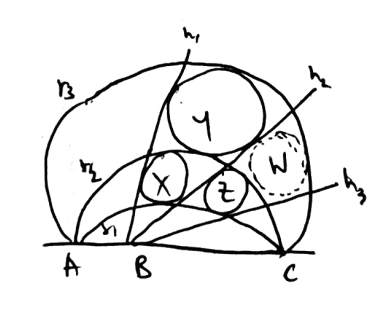
ISL 2010 G7: Three circular arcs $\gamma_1, \gamma_2,$ and $\gamma_3$ connect the points $A$ and $C.$ These arcs lie in the same half-plane defined by line $AC$ in such a way that arc $\gamma_2$ lies between the arcs $\gamma_1$ and $\gamma_3.$ Point $B$ lies on the segment $AC.$ Let $h_1, h_2$, and $h_3$ be three rays starting at $B,$ lying in the same half-plane, $h_2$ being between $h_1$ and $h_3.$ For $i, j = 1, 2, 3,$ denote by $V_{ij}$ the point of intersection of $h_i$ and $\gamma_j$ (see the Figure below). Denote by $\widehat{V_{ij}V_{kj}}\widehat{V_{kl}V_{il}}$ the curved quadrilateral, whose sides are the segments $V_{ij}V_{il},$ $V_{kj}V_{kl}$ and arcs $V_{ij}V_{kj}$ and $V_{il}V_{kl}.$ We say that this quadrilateral is $circumscribed$ if there exists a circle touching these two segments and two arcs. Prove that if the curved quadrilaterals $\widehat{V_{11}V_{21}}\widehat{V_{22}V_{12}}, \widehat{V_{12}V_{22}}\widehat{V_{23}V_{13}},\widehat{V_{21}V_{31}}\widehat{V_{32}V_{22}}$ are circumscribed, then the curved quadrilateral $\widehat{V_{22}V_{32}}\widehat{V_{33}V_{23}}$ is circumscribed, too.

To make the internal/external tangencies work, we put $\gamma_1,\gamma_3$ in the future and $\gamma_2$ in the past.

Because $\gamma_1,\gamma_2$ have a common chord, they are time-like separated and intersect along an ellipse, which lies on a plane $\Pi$ through $AC$. Similarly, $\gamma_2,\gamma_3$ intersect on a plane $\Pi'$ through $AC$.

Now let's think about the locus of circles which are tangent to $h_1,h_2$ (in the sector contained in the relevant half-plane). These are a line $\ell$ and its reflection $\ell'$ across the present plane.

The fact that $X$ and $Y$ exist means that $\ell$ and $\ell'$ lie on $\Pi$ and $\Pi'$ respectively (or vice versa). So the reflection of $\Pi'$ across the present intersects $\Pi$ on $\ell$ and on $AC$, so they must be equal, i.e. $\Pi,\Pi'$ are reflections of each other across the present.

Do the same thing but for $h_2,h_3$ to get two lines $m,m'$. But then $m$ lies on $\Pi$ as $Z$ exists, so $m'$ lies on $\Pi$, implying the existence of $W$! $\square$

In fact, the exact same method proves the generalisation here:

3.2 Another generalisation

Edit (21/4/2024): This was originally meant to be part of the post, but I couldn't find a satisfactory way to handle the $h_i$ without some amount of bash, so I omitted it. However, this resulted in all the theory developed above regarding Lorentz transformations becoming useless (the ISL G7 can be solved without considering the relativistic structure of $\mathbb{R}^{2+1}$, just using the ideas from the introduction), which I found profoundly unsatisfying. As a result, I ended up thinking about this (very) intermittently and eventually figured out how to fix my solution.

The generalisation in question is the one mentioned in Post #5:

Under the same assumptions as before, the curved quadrilateral $\widehat{V_{11}V_{31}}\widehat{V_{33}V_{13}}$ is also circumscribed.

For our approach to work, we need $\gamma_1,\gamma_3$ to be on opposite sides of the present. We resolve this by putting $\gamma_1$ in the future, $\gamma_3$ in the past, and having two copies of $\gamma_2$, one in the future and one in the past:

Then, by the arguments above, the ellipses $\gamma_1 \cap \gamma_2'$ and $\gamma_2 \cap \gamma_3'$ lie on a common inertial frame $\Pi$ through $AB$. We want to show that, as above, the line corresponding to the locus of circles tangent to $h_1,h_3$ lies in the plane $\overline{\Pi}$ containing $\gamma_1\cap \gamma_3'$.

Perform a Lorentz transformation so $\Pi$ is now the present. Then, our picture must look like this:

Hence, what used to be the present plane (the plane containing $\gamma_2 \cap \gamma_2'$) is now the reflection of $\overline{\Pi}$ across the new present plane!

Let's look again at the $h_i$. As constructed earlier, let $\ell_{12}$, $\ell_{23}$, and $\ell_{13}$ be the lines on $\Pi$ representing the loci of circles tangent to $h_1,h_2$,  $h_2,h_3$, and $h_1,h_3$ respectively. Note that $\ell_{13}$ is the intersection of the planes $\Pi_1$ through $h_1,\ell_{12}$ and $\Pi_2$ through $h_3,\ell_{23}$.

Consider the plane through $h_1, \ell_{12}$. This is a plane making an angle of $\frac\pi4$ with the present. We claim that after a Lorentz transformation, this plane still meets the (new) present at an angle of $\frac\pi4$. The way I see this is that every such plane is a common tangent plane of two light cones, and this property is preserved by Lorentz transformations. The same goes for all the relevant "diagonal" planes.

Hence, after applying our Lorentz transformation, $\ell_{12},\ell_{23}$ lie in the present, and $h_2$ is the locus of circles tangent to both of these lines. Moreover, $\Pi_1$ is now the reflection of the plane through $h_2,\ell_{12}$ across the present, and likewise $\Pi_2$ is the reflection of the plane through $h_2,\ell_{23}$. Hence, $\ell_{13} = \Pi_1 \cap \Pi_2$ is the reflection of $h_2$ across the present.

But since $h_2$ is in the old present, i.e. the reflection of $\overline{\Pi}$ across the new present, then $\ell_{13}$ indeed lies in $\overline{\Pi}$. $\square$

4 Conclusion

I hope I've shown that special relativity is pretty cool and that being forced to take a physics course isn't always a bad thing. In general, because of how symmetrical the laws of physics are, physics does tend to provide motivation for certain structures in math; another example that immediately comes to mind is the spin representation. I think it's pretty cool how you can take an idea from physics and derive a whole bunch of math from it.

Also, if you missed the meta-commentary section above, geometric transformations are great! They let you exploit symmetries of the universe to view configurations in a new light.

Anyway, if you've enjoyed the stuff here, you might want to look at the other Section 8 theorems in Skutin's 2017 paper or his absolutely bonkers generalisation of the Feuerbach point, which I haven't yet managed to prove. If you do manage to prove them, I'd be happy to hear from you!