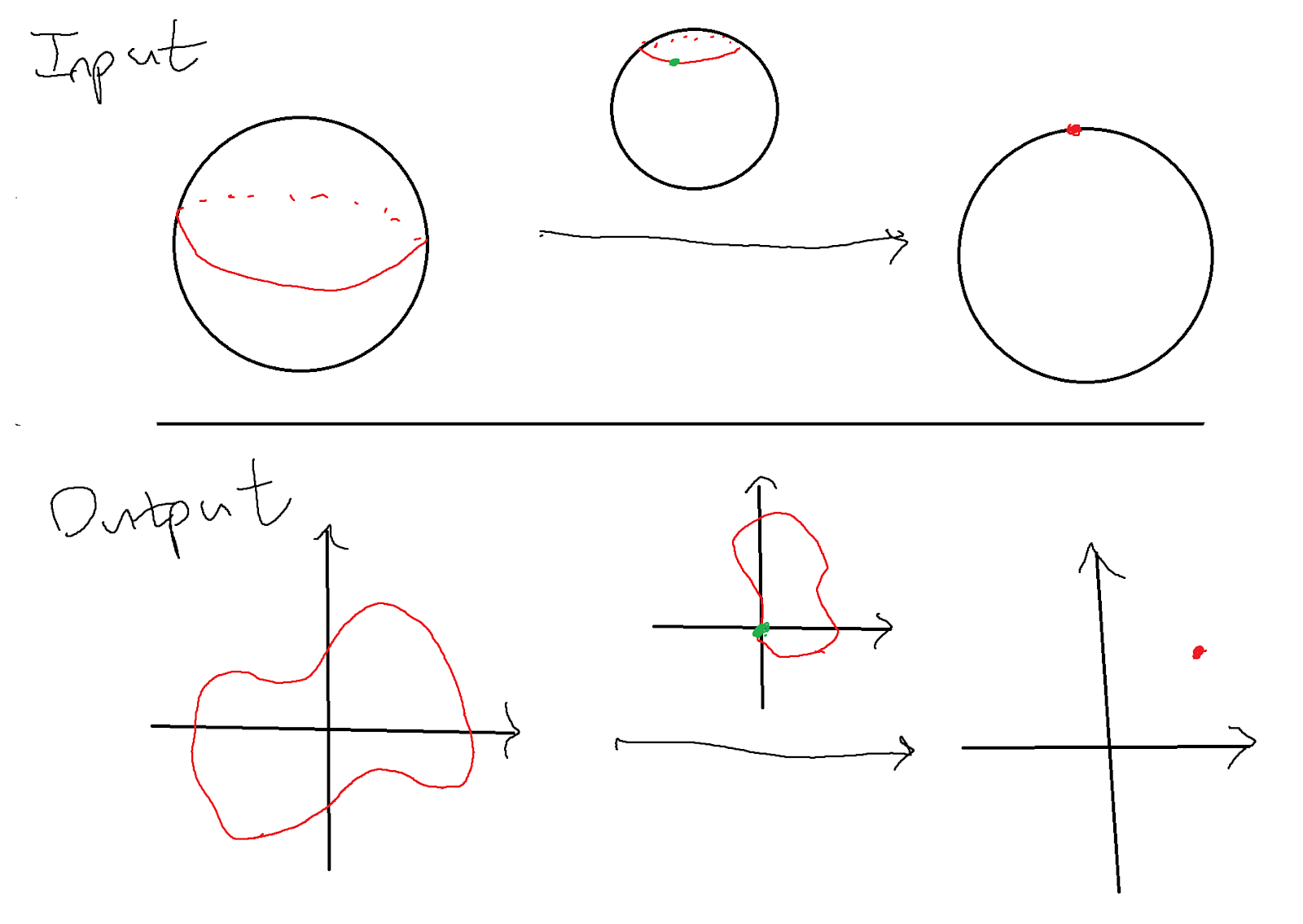SIMO Retiree Blog

 (Jit here). There is a famous theorem of Lagrange that says every natural number $n$ is a sum of four non-negative squares (so that $0$ is allowed). Let's try to prove this theorem.

Introduction Etienne here. Some of my favourite proofs in mathematics are those that connect two seemingly unrelated subfields together. A well-known example of this is Andrew Wiles' proof of Fermat's Last Theorem, which uses a special connection between elliptic curves and modular forms. In this article I'll demonstrate some bizarre proofs using topology, the study of continuous transformations, in the field of combinatorics, the study of discrete objects.

Hi, this is Choo Ray. I have been conducting trainings quite a bit recently, so I have forced myself to get better at understanding the key points of solutions in a manner which I can convey to others. The difficulty is that math olympiad takes time . I am lucky if I get to try all the problems in a problem set I create, much less solve them. However, I still need to have a good enough understanding of the problem to gather the important ideas and teach them to others.

(David here.) I'm going to explore various versions of an idea, starting from where I first saw it in Olympiads, and going beyond.