Who's Afraid of Topological Proofs?
Introduction
Etienne here. Some of my favourite proofs in mathematics are those that connect two seemingly unrelated subfields together. A well-known example of this is Andrew Wiles' proof of Fermat's Last Theorem, which uses a special connection between elliptic curves and modular forms. In this article I'll demonstrate some bizarre proofs using topology, the study of continuous transformations, in the field of combinatorics, the study of discrete objects.
This article will focus specifically on applications of the Borsuk-Ulam Theorem, which goes as follows:
(Borsuk-Ulam) For any continuous function $f:S^n\rightarrow \mathbb R^n$, there is a pair of antipodal points that have the same value.
Here, $S^n$ is the unit $n$-sphere, which is the boundary of the unit sphere that looks likes it's in $n$ dimensions for a person standing on it. For example, a circle is a $1$-sphere (to a small ant it would seem like a line), and the surface of the earth is a $2$-sphere, because it looks flat to most people. You can also think of it as $2D$ because on the surface of the Earth, we're actually constrained to only $2$ dimensions. A popular version of the Borsuk-Ulam Theorem for $n=2$ states that there are two antipodal points on the Earth that have the same temperature and pressure.
You can think about why this is true. For $n=1$, suppose there's a function $f$ taking values on a circle, and consider two antipodal points $A,B$. If they have the same value, we're done; otherwise, suppose $f(A)<f(B)$ and consider two ants starting at each point and travelling clockwise at the same speed, so they are always antipodal. Then when the ants switch positions, $f(A)-f(B)$ changes sign, so it crosses $0$ at some point.
It's the same idea for $n=2$. Consider two functions $f,g$ that take real values on $S^2$. Now consider $h(A)=\left(f(A)-f(-A),g(A)-g(-A)\right)$ as we move around the sphere. Note that $h(-A)=-h(A)$, so we just have to prove that $h(A)=0$ at some point. Again, we consider a great circle that contains $A$ and $-A$, and imagine walking on this circle. As we walk in a loop on this circle, we output a loop in $2$ dimensions that is symmetric about the origin. Now imagine contracting the circle on the sphere to a point. This is a continuous process, and our output loop also contracts to a point. At some point, it must pass through the origin, and this is our desired point.
Some Classical Applications of Borsuk-Ulam
The Ham Sandwich Theorem
Before we venture into discrete math, let's try proving something more continuous first. This theorem states the following:
(Ham Sandwich) Given any $n$ (measurable) bodies in $\mathbb R^n$, we can find a $(n-1)$-dimensional hyperplane that bisects them.
Our method of attack is to somehow consider the $(n-1)$-sphere $S^{n-1}$ that exists in $\mathbb R^n$, and to find a continuous function that takes $n-1$ values at each point.
Let's consider a $(n-1)$-hyperplane that bisects one of the $n$ bodies in $\mathbb R^n$. We can find one of these using the intermediate value theorem by moving our hyperplane through the body like a scanner. Since this hyperplane also splits $\mathbb R^n$ into two, let's assign it one of these by considering the normal vector in that direction. Now we can biject this vector to the normal vector that defines a point on $S^{n-1}$, so we have a continuous bijection from hyperplanes to points on the sphere.
Now we just need to find $n-1$ values that vary continuously, which we can do by considering the volume of the other $n-1$ bodies in the region of space that we chose. Then by the Borsuk-Ulam theorem, there must be two antipodal points which have the same value. Since each pair of antipodal points maps to the same hyperplane with a different direction, this means that the hyperplane splits every body with equal volume on both sides, so we're done.
Splitting a Stolen Necklace
This is probably the most famous application of the Borsuk-Ulam theorem, because 3Blue1Brown made a video on it a few years back.
The problem is as such:
(Necklace Splitting) Two thieves steal a string that contains some beads of $n$ types, such that there is an even number of each type. Find the minimum $k$, such that the thieves can always make at most $k$ cuts in the string and distribute the $k+1$ substrings such that each thief receives exactly half of each type of bead.
The reader may pause and ponder what the value of $k$ might be. Our main idea is now to turn our discrete problem into a continuous one. Instead of beads, we will consider coloured intervals of length 1 on a line. Now imagine moving $k$ cuts around. The length between each cut is now continuous.
We can easily go back to the discrete case, since, if a cut is in an interval, if the subinterval on both sides of the cut go to the same person, we can remove it. Otherwise, since each person receives an integral length of each colour, there must be another cut that goes through an interval of the same colour; we can then smooth both of these either towards or away from each other such that one of them reaches an integer. We repeat this process, and eventually all cuts are between intervals.
Now I will reveal the value of $k$: it is in fact $n$. Now that we have proven the validity of our continuous problem, let's change it to having $n+1$ subintervals on an interval of length $1$. This is represented by the equation $$x_1+x_2+\cdots+x_{n+1}=1$$ which one can note is similar to the equation for the unit $n$-sphere: $$x_1^2 +\cdots+x_{n+1}^2=1$$ So we can map each set of $n$ cuts to a point on the $n$-sphere, except that each $x_i$ may be positive or negative on the sphere. Therefore, we let the sign of each $x_i$ determine which thief that subinterval goes to. One can check that this mapping is continuous, and that swapping the ownership of every subinterval corresponds to going to the antipode in our output space.
It should be relatively clear what our function from to $\mathbb R^n$ should be. For each colour, we'll take the length of that colour that thief 1 receives minus that that thief 2 receives. This gives us $n$ values. Since swapping ownership of all pieces changes the sign of each value (i.e. $f(-A)=-f(A)$), the Borsuk-Ulam theorem guarantees that there is some point whose output in $\mathbb R^n$ is $0$, which is precisely the solution we seek. Interestingly, all known proofs of this theorem use topological methods.
Interested readers can prove that $n-1$ cuts is insufficient for some configuration of beads.
Finale: Chromatic Number of the Kneser Graph
This is the problem which started the whole field of topological combinatorics. It was first given a topological solution by Lovász, who is also known for his local lemma from probability.
Given a set $S$ of $n$ elements, the Kneser Graph $KG(n,k)$ has vertices as $k$-element subsets, and two vertices are adjacent if their corresponding subsets are disjoint. We will prove that the chromatic number of this graph, which is the minimum number $\chi$ such that the vertices can be coloured in $\chi$ colours with no two adjacent vertices having the same colour, is $\text{max}(n-2k+2,1)$. Of course, this is only interesting when $n\ge 2k$, since there are no edges when $n<k$, so we'll suppose that $n\ge 2k$ from now on.
To prove this fact, we need a corollary of the Borsuk-Ulam Theorem, sometimes called the Lusternik-Schnirelmann-Borsuk (LSB) Theorem, which goes as follows:
(LSB) For any covering of $S_{n}$ with $n+1$ closed sets, there is a set which contains two antipodal points.
This can be proven in much the same way as the previous two examples. We'll first take $n$ closed sets labeled $1,2,\dots,n$, and for every point on the sphere, take $d_i$ to be the closest distance on $S^n$ to the $i$th set. If the point is in the set, the distance is $0$. This defines a continuous function from $S^n$ to $\mathbb R^n$, so by the Borsuk-Ulam Theorem, there are two points which have the same distance to each set. If $d_i=0$ for any specific $i$, then these points lie in the same set. Otherwise, $d_i>0$ for each $i$, and so these two points must lie in the $(n+1)$th set.
The proof uses a slightly stronger form of the theorem, which allows each of the $(n+1)$ sets to be either open or closed. This can be proven using a bit of topology magic, which I won't go into. Instead, I'll get right into the meat of the proof.
Suppose there were a colouring of the graph with $n-2k+1$ colours. Let $d=n-2k+1$. Now consider $n$ points lying on $S^d$ such that no $d+1$ of them share a hyperplane with the center of the circle (since $S^d$ is a subset of $\mathbb R^{d+1}$). We biject each of these points to an element of the set, and now consider all tuples of $k$ points.
We'll define the open sets $A_1,\dots,A_d\subseteq S^d$ as such: For any $x\in S^d$, $x$ is in $A_i$ the open hemisphere centered at $x$ contains a $k$-tuple of points coloured with colour $i$. This is easier to imagine if you first imagine the $k$-tuple of points, and then swirling a hemisphere around it. Our last set will simply be the complement of all the sets, i.e. $$A_{d+1}=S^d\,\backslash \left(\bigcup_{i=1}^dA_i\right)$$ which is closed (because the complement of an open set is closed).
These $d+1$ sets form a cover of $S^d$. Then by the LSB theorem, one of these sets contains two antipodal points. If it's one of $A_1,\dots,A_d$, then there are two $k$-tuples in opposite hemispheres with the same colour. But they are clearly disjoint and so connected by an edge, which is a contradiction.
So it must be in $A_{d+1}$. Note now that any open hemisphere centered at a point in $A_{d+1}$ contains at most $k-1$ points, since otherwise this point would belong to one of the $d$ sets. Then consider the two open hemispheres that are centered at the antipodes contained in $A_{d+1}$. These contain at most $2k-2$ points, so now consider the complement of their union, which is a great $(d-1)$-sphere (Consider the $d=2$ case: the complement of two open hemispheres centered at antipodes is a great circle) There are at least $n-2k+2=d+1$ points on this great sphere, which means that there are $d+1$ points which lie on a hyperplane passing through the origin. Contradiction!
Interested readers are welcome to try prove that the chromatic number of $KG(n,k)$ is at most $n-2k+2$.
Bonus: Applications of the Ham Sandwich Theorem
As a recap, the ham sandwich theorem states that given $n$ bodies in $n$-dimensional space, one can find a $(n-1)$-hyperplane that bisects all of them. We'll need to use a discrete version of this for the following problems.
(Discrete Ham Sandwich) For $n$ sets of points in $\mathbb R^n$, there is a $(n-1)$-hyperplane that bisects each set, which means that for each set $S$, at most $\left\lfloor\frac {|S|}2\right\rfloor$ points lie on each side of the hyperplane.
This is easily proven from the continuous version by taking a small ball around each point, and shrinking it to $0$, which is, of course, a continuous process. What's annoying about this theorem is that it's possible for many points to lie on the hyperplane. Luckily, there's a fix.
(Refined Ham Sandwich) For $n$ sets of points in $\mathbb R^n$ such that no $n+1$ points share a hyperplane, we can choose a hyperplane such that for each set $S$, there are exactly $\left\lfloor\frac {|S|}2\right\rfloor$ points of each side on the hyperplane.
We can prove what I'll call the "Refined Ham Sandwich Theorem" from the discrete form as follows: Take the hyperplane that the discrete form gives us, and if there are less than $n$ points on it, we'll add a set of dummy points $D$ so that there are exactly $n$ points on this hyperplane. Then, each set $S$ has an even number of "unwanted" points on this hyperplane, so we'll pair them up, and for each pair, we move one by $\varepsilon \hat n$ and the other by $-\varepsilon \hat n$, where $\hat n$ is the normal to the hyperplane. The rest of the points we keep. Then we take the hyperplane that passes through the new points and the dummy points, of which there are $n$ in total. As $\varepsilon\rightarrow 0$, the hyperplane grows closer to the original one, and for some sufficiently small $\varepsilon$ this movement does not affect any points not on the original hyperplane.
Now, let's finally apply this to some Olympiad problems.
(Folklore) There are $n$ red and $n$ blue points in the plane. Prove that there is a matching of red and blue points such that no line segments intersect.
We'll prove this by strong induction. By the Refined Ham Sandwich theorem, there is a line that bisects each set of red and blue points. If $n$ is even, the line divides the points into two smaller cases which clearly don't interact with each other. If $n$ is odd, there is one red and one blue point on the line, which we can connect, and two smaller cases. So we are done.
(Old Russia) Inside $100$ boxes, there are some apples, bananas, and cherries. Prove that one can select $51$ boxes such that they contain at least half of all apples, half of all bananas, and half of all cherries.
This is a pretty difficult problem I gave in a training session recently, and I encourage the reader to try and find the combinatorial proof. Fortunately, there is a proof using the ham sandwich theorem.
Represent these $100$ boxes as cubes in $\mathbb R^3$ such that no plane passes through any four of these (this is clearly possible), with fruits being points in these cubes. By the Discrete Ham Sandwich Theorem, there is a plane that bisects the sets of apples, bananas, and cherries, passing through at most $3$ boxes. We take the side with the smaller number of boxes, and any boxes that lie on the plane. This adds up to at most $48+3=51$.
(Necklace Splitting) Two thieves steal a string that contains some beads of $n$ types, such that there is an even number of each type. Find the minimum $k$, such that the thieves can always make at most $k$ cuts in the string and distribute the $k+1$ substrings such that each thief receives exactly half of each type of bead.
Attentive readers might notice that we had already proved earlier that $k=n$. However, there is another proof that I couldn't resist mentioning. We'll put our string in $\mathbb R^n$ on the curve parametrised by $(x,x^2,\dots,x^n)$. The key idea is that any hyperplane intersects this curve in at most $n$ points. Since a hyperplane is defined by a linear combination of each variable, we have that for each intersection point, $$a_1x+a_2x^2+\cdots+a_nx^n=c$$which is just a polynomial of degree $n$, so there are at most $n$ of these.
Then using the Refined Ham Sandwich Theorem on the $n$ types of beads, there is a hyperplane that splits each type cleanly and that cuts this string in at most $n$ points, so we're done.
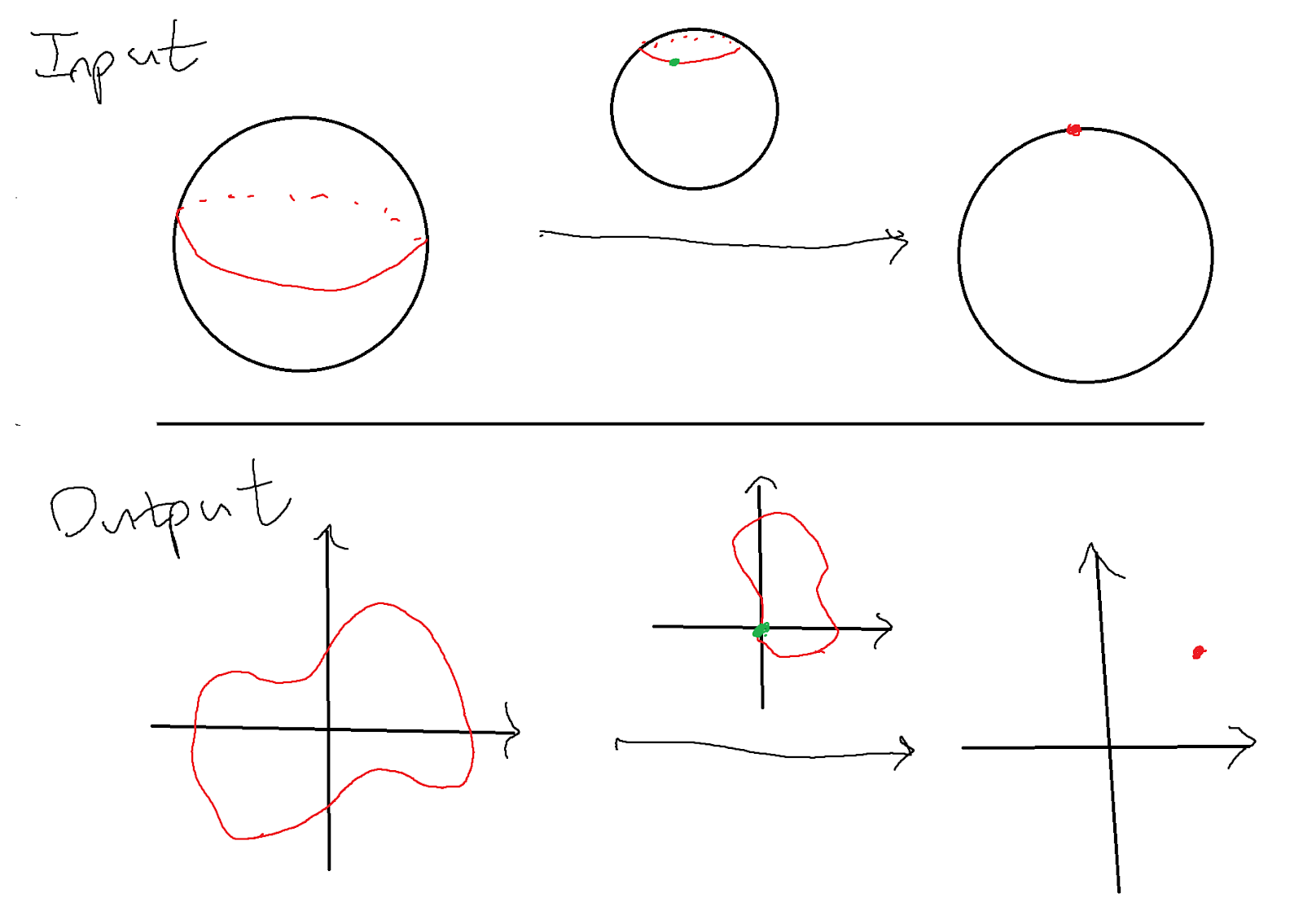








Comments
Post a Comment