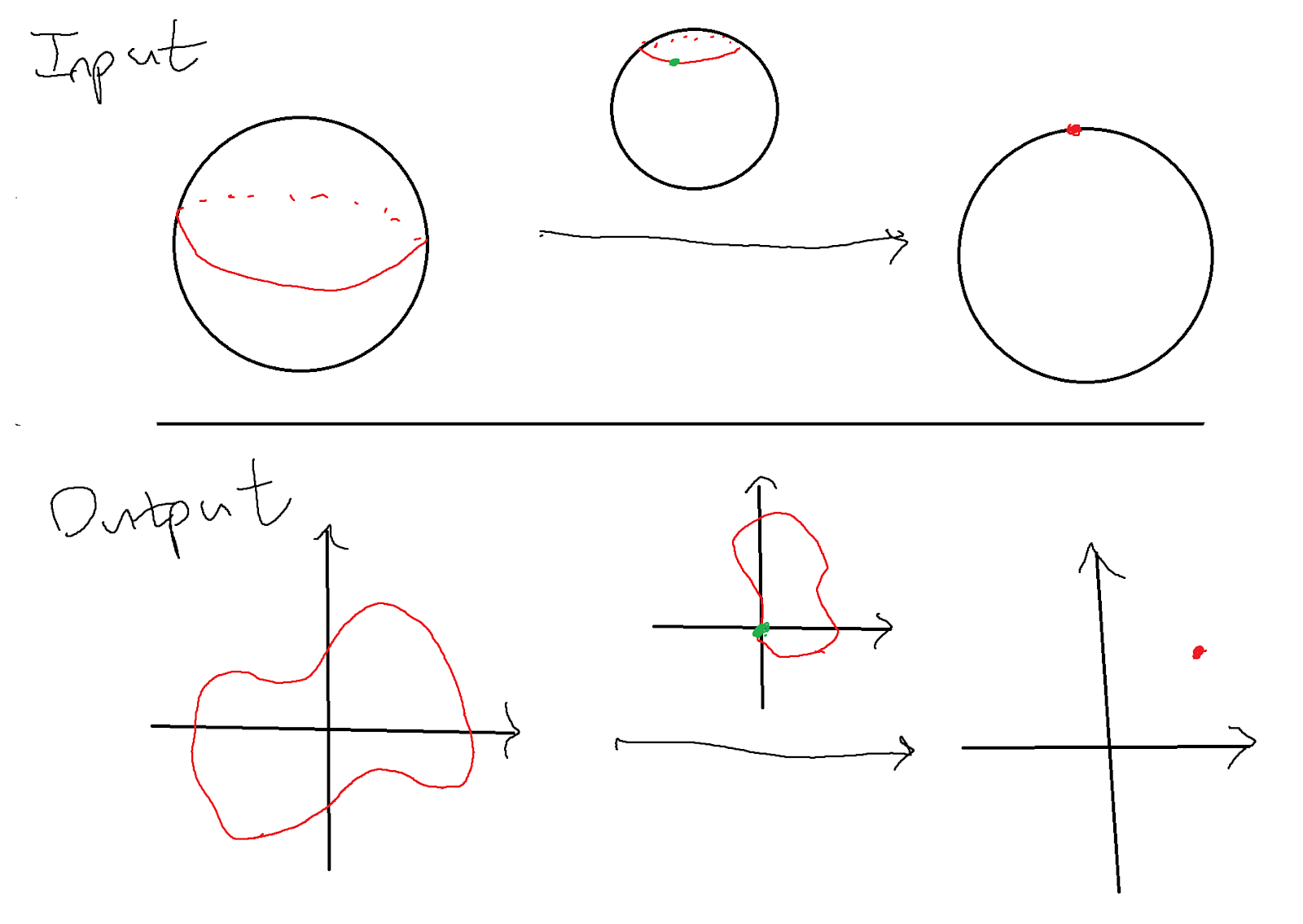SIMO Retiree Blog

 (Jit here). There is a famous theorem of Lagrange that says every natural number $n$ is a sum of four non-negative squares (so that $0$ is allowed). Let's try to prove this theorem.

Introduction Etienne here. Some of my favourite proofs in mathematics are those that connect two seemingly unrelated subfields together. A well-known example of this is Andrew Wiles' proof of Fermat's Last Theorem, which uses a special connection between elliptic curves and modular forms. In this article I'll demonstrate some bizarre proofs using topology, the study of continuous transformations, in the field of combinatorics, the study of discrete objects.

Hi, this is Choo Ray. I have been conducting trainings quite a bit recently, so I have forced myself to get better at understanding the key points of solutions in a manner which I can convey to others. The difficulty is that math olympiad takes time . I am lucky if I get to try all the problems in a problem set I create, much less solve them. However, I still need to have a good enough understanding of the problem to gather the important ideas and teach them to others.

(David here.) I'm going to explore various versions of an idea, starting from where I first saw it in Olympiads, and going beyond.

(Xu Chen here) Today I am going to talk about a subtle but important thought process for many problems, which is how you visualize the objects you are working with. This is more of an intuitive idea than rigorous math, so forgive me if not everything is super clear in this post. How you look at the problem can heavily influence what ideas you can come up with: The solution often follows from a good understanding of the underlying structure. Example 1. Let's start with a simple example. (USAJMO 2019/2) Let $\Z$ be the set of all integers. Find all pairs of integers $(a,b)$ for which there exist functions $f:\Z\to\Z$ and $g:\Z\to\Z$ satisfying $$f(g(x))=x+a\quad \text{and}\quad g(f(x))=x+b$$ for all integers $x$. Hopefully it is clear that we cannot treat this as a standard FE, but must instead consider some combinatorial ideas. Let's think of $\Z$ on the number line. We draw red arrows to represent $x\mapsto f(x)$ and blue arrows to represent $x\mapsto g(x)$: One cond...

(This is Yan Sheng.) $\newcommand{\bb}{\mathbb}\newcommand{\Con}{\operatorname{Con}}$I once read this mind-bending blog post by Joel David Hamkins that proves this result: Theorem : There is a Turing machine program $P$ such that for any function $f:\bb N\to\bb N$, there is a model of Peano arithmetic in which $P$ computes $f$ on the standard natural numbers. Read that again: there is a single Turing machine that outputs any given function—even uncomputable ones (!!)—if you run it in the correct universe. If this statement doesn’t surprise you, I’m not sure what else would (unless you work in logic or set theory; I’m convinced that those people routinely believe as many as six impossible things before breakfast ). A extraordinary claim needs an extraordinary proof, and when I read through Hamkins’s argument I came across a lesser absurdity: a theory that proves its own inconsistency. Since all my knowledge of formal logic is from folklore, this post is my attempt to informal...

(David here.) In The Rising Sea , Ravi Vakil writes: When introduced to a new idea, always ask why you should care. Do not expect an answer right away, but demand an answer eventually. Try at least to apply any new abstraction to some concrete example you can understand well. We have something analogous for understanding proofs - with time, new perspectives show up and reveal new insight, and allows one to tackle problems that seemed impossible before.