SMO Open 2023 ??% Speedrun

(This is Glen.)

I'm doing this since I'm relatively free at the moment (it's still summer vacation) and I've been looking for an excuse to try these problems anyway. I'll give myself 4 hours (which I think is the duration of the competition?), type everything I'm thinking of in bullet points and add headers to make things more readable at the end. I'm not writing out solutions properly because the focus is on the thought process rather than the actual solution but the intent is that the solution is still discernable if you follow everything I write down. All in all, the time saved in not having to write things nicely should cancel out with the extra time I spend typing out all of my thoughts. Anyway, here I go. Let's hope I don't embarrass myself.

Problem 1

In a scalene triangle $ABC$ with centroid $G$ and circumcircle $\omega$ centred at $O$, the extension of $AG$ meets $\omega$ at $M$; lines $AB$ and $CM$ intersect at $P$; and lines $AC$ and $BM$ intersect at $Q$. Suppose the circumcentre $S$ of the triangle $APQ$ lies on $\omega$ and $A,O,S$ are collinear. Prove that $\angle AGO = 90^\circ$.

Initial thoughts/observations

• Why is SMO Q1 always geometry.
• It's conditional geometry, which means it's a bit harder (though not impossible) to bash. Oh wait, there are two conditions...sigh.
• Ok, I just drew out the diagram. (I guess I'll scan in pictures when I'm done?) The point $M$ is quite weird, but it's nice if you inverflect it (foot of symmedian on side $BC$). But that feels like overkill.

Glen from the future: here's the diagram, as promised. There's some other stuff that I added in the later steps.

Some observations, and conveniently, a solution

• I want to say that $A,O,S$ collinear implies $PQ||BC$; the intuition is that $AO$ is fixed by zooming in and out at $A$ ("homothety"), so you can WLOG move $P$ to coincide with $B$ and scale $Q$ by the same amount...oh ok that works.
• So formally: homothety at $A$ sends $(ABC)$ to $(APQ)$ and sends the lines $AB$, $AC$ to themselves, so taking intersections, $BC$ is sent to $PQ$, yay.
• $BC||PQ$ also implies $A,O,S$ collinear, so we can replace the latter with the former, and throw away the point $S$...wait no there's still the other condition.
• I thought the $\angle AGO$ thing would be some horrible thing to do with the Euler line, but I'm now realising that this is just saying that $AG=GM$.
• We also know $G$ is $\frac23$ of the way from $A$ to midpoint $BC$ (call it $N$), so we just want to show $GN=NM$, i.e. $BGCM$ is a parallelogram.
• Ok, we haven't used the fact that $S$ is on $(ABC)$. Oh, but $S$ has to be the point diametrically opposite $A$, which means the homothety from $ABC$ to $APQ$ is by a factor of $2$.
• So we'd be done if the homothety sent $G$ to $M$ (so the bit I wrote above about the parallelogram is useless). Oh, that's true, since $B$ is the midpoint of $AP$ and $C$ the midpoint of $AQ$, so $M$ is the centroid of $APQ$. Cool.

Time check: 14 minutes.

Problem 2

A grid of cells is tiled with dominoes such that every cell is covered by exactly one domino. A subset $S$ of dominoes is chosen. Is it true that at least one of the following 2 statements is false? (1) There are $2022$ more horizontal dominoes than vertical dominoes in $S$. (2) The cells covered by the dominoes in $S$ can be tiled completely and exactly by $L$-shaped tetrominoes.

Initial thoughts/observations

• "Is it true that at least one of the following statements is false" is such weird wording, but essentially we're being asked if both statements can be simultaneously true. So either we want to construct an example in which both are true, or assume one is true and show the other is false.
• Ok, let's try to construct stuff. We could arrange $2$ horizontal dominoes and $1$ vertical domino into a $2\times3$ rectangle, and then glue $2022$ of these rectangles to get a $2$ by something rectangle, which seems like a nice shape? On the other hand, two L-shaped tetrominoes form a $2\times4$ rectangle, so we want $4$ to divide the something, which is, uh, $3\times 2022$, no bueno. This does tell us that we'd be done if $2022$ were a multiple of $4$.
• Presumably the solution isn't actually "here's a construction, hahahaha done" so I'm guessing the answer is it doesn't work if $n$ (horizontal minus vertical) is $2\pmod4$ and works if it's $0\pmod4$. If $n$ is odd...oh then it fails because you have an odd number of dominoes which cover a $2\pmod4$ number of squares.
• Assuming this is true, we could try to replace $2022$ by $2$ to make our lives easier.

Attempt at solution

• The general solution looks like some funny parity thing, which suggests some sort of black/white colouring.
• The way you usually deal with L shapes is to colour in stripes, so let's try that. Suppose we colour in vertical stripes, and there are $a$ vertical dominoes. So the number of tetrominoes is $\frac{a+1011}2$, so $a$ is odd. Each L domino contributes $\pm2$ to the number of white minus the number of black, each horizontal one contributes evenly, and each vertical contributes $\pm2$. Taking mod $4$ means there's an odd number of L dominoes? So $a\equiv 3\pmod 4$? That isn't very useful. Unless I tried to do some sort of $v_2$ induction...ew.
• At this point, I realise I'm subconsciously thinking of the problem as: there are a bunch of L-shaped tetrominoes, show that you can't cover them with dominoes such that there are $2022$ more horizontal than vertical. This is slightly weaker than the original version (requiring the whole grid to be tiled) because you might want to rule out cases where the L-shaped tetrominoes surround a hole with an odd number of squares or something. Let's hope it doesn't come to that.

Actual solution

• Ok, let's look back at the failed construction. If we just greedily fill up the $2\times$whatever rectangle with $2\times4$s, we're left with a $2\times2$ square. So maybe we want a colouring to distinguish between that and an L shape.
• I guess we could just do the standard $4$-colouring: $4$-colour a $2\times2$ square and tile the plane. That distinguishes the square and the L shape since the former uses colours evenly and the latter doesn't.
• Now what.
• Sigh, when all else fails, we can probably just bash simultaneous equations. Let $a$ be the number of dominoes covering colours $1,2$, $b$ the number covering $3,4$, $c$ the number covering $1,3$, $d$ for $2,4$. Let $A$ be the L shapes with two $1$s, a $2$ and a $3$, $B$ for 2 $2$s, etc.
• So comparing by colour, we have $a+c = 2A + B + C$ and symmetric equivalents.
• Can we get $a+b-c-d$? This is the same as asking if $(1,-1,1,-1)$ is in the span of $(1,1,0,0),(0,1,1,0),(0,0,1,1),(1,0,0,1)$, which are obviously linearly dependent...uh...ok the four vectors dot with $(1,-1,1,-1)$ to give $0$ but $(1,-1,1-1)$ dots with itself to give $4$, so no.
• Well we could take it mod $4$, that fixes things.
• Aha, working in mod $4$, we have $a+b-c-d = (a+c) + 2(b+c) + 3(b+d) = (2A+B+C) + 2(A+2C+D) + 3(B+C+2D) = 2A + B + C + 2A + 2D - B - C + 2D = 0$, yay!
• Ok so that was horrible motivation; presumably a better train of thought would be: the final answer is in terms of mod $4$, so work in mod $4$.

Time check: 44 minutes.

Problem 3

Let $n\ge 2$ be a positive integer. For a positive integer $a$, let $Q_a(x) = x^n + ax$. et $p$ be a prime and let $S_a = \{b|0\le b\le p-1, \exists c\in \mathbb Z, Q_a(c) \equiv b \pmod{p}\}$. Show that $\frac1{p-1}\sum_{a=1}^{p-1} |S_a|$ is an integer.

Initial thoughts/observations

• What on earth is that symbol salad? Ok, it's just the number of values $Q_a$ takes when you cycle through $x\pmod{p}$. And you want $p-1$ to divide the result when you sum over $a$.
• I guess you'd expect that to be $n$ minus some error terms?
• Maybe I should try some small cases but that seems so boring; I'll do it when I get stuck.
• I'm thinking it could be some sort of double counting thing where you write values in a table...something like the proof of quadratic reciprocity? I forgot the proof of quadratic reciprocity. There was something about a grid. Nvm.

Trying small cases

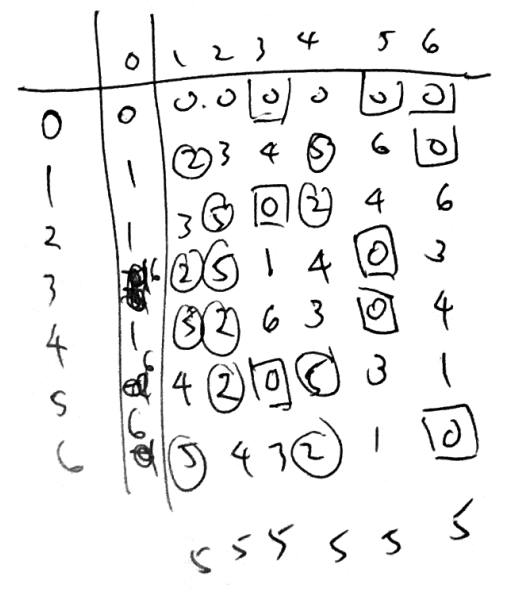
• Ok, let's try, say, $p=5,n=7$. Oh, wait a second, FLT lets you assume $1 \le n \le p-1$. Ok so my second bullet point is egregiously wrong but maybe not wrong with the extra condition.
• Anyway, let's try $p=5,n=3$. I'm just going to scan the table in; you get four $3$s.

$p=5,n=3$. Yes, I am that bad at arithmetic.

• Something I stupidly didn't notice is that things vary linearly across rows.
• Ok, I'm stuck, so I'm going to draw more tables.`

$p=2,n=1$; $p=3,n=1$; $p=3,n=2$; $p=5,n=2$.

• I should have noticed this earlier, but every row other than the first is $0$ to $p-1$ in some order (because of the linearity thing). Also, presumably the $n=1,p-1$ cases should be obvious by direct computation.

Getting an idea of an approach

• Maybe instead of counting distinct values, we can count repeats: we want to show the number of "extra numbers" is divisible by $p-1$.
• Oh, the lines all have different gradients, so for "$p$ prime" reasons, each pair intersects exactly once.
• But we also want to subtract the number of repeats in the first column, which is, uh, something related to $\gcd(n,p-1)$ because something something primitive roots.
• Oh wait this counting method gets wonky when multiple things intersect in the same column. Let's try $p=7,n=3$.

$p=7,n=3$.

• Seems like beyond the first column (actually maybe I should have been calling this the zeroth column), the only repeats with multiplicity $>2$ are the $0$s. Is that true in general? Surely that's too good to be true. Let's try $n=4$ instead.

$p=7,n=4$.

• Ok so it's somehow true??
• Actually, maybe we can just calculate it. Let $x^n + ax \equiv y^n + ay \pmod{p}$. Then $a \equiv (x-y)^{-1}(y^n-x^n) \pmod{p}$. I want to say this is $-x^{n-1} - x^{n-2}y - \ldots - y^{n-1}$... yeah I think that's true except when $x^n \equiv y^n \pmod{p}$, which is exactly the column we don't care about. Looks promising.
• So we substitute this value of $a$ in and get something like $-xy \times \frac{x^{n-1} - y^{n-1}}{x-y}$, which is nonzero when $x,y$ are nonzero and $x^{n-1},y^{n-1}$ are different mod $p$. So now assume $x^{n-1} + x^{n-2}y + \ldots + y^{n-1} = x^{n-1} + \ldots + z^{n-1}$. WLOG $x$ not $0$ otherwise we get the $0$ case, so we can divide by $x^{n-1}$, and we get $\left(\frac{y}x\right)^{n-1} + \ldots + 1 = $ same thing but for $z$, and we want...first terms on each side to be equal? Seems sus.

Trying another approach

• Ok, but maybe some ratio thing would work. Suppose rows $1$ and $x$ intersect at $a$, then $r,rx$ intersect at $r^{n-1}a$ using the formula above.
• That means there has got to be some matchy-matchy thing going on; columns are related if their ratios are some power of $n-1$ mod $p$, which means I might have to go back and figure out how the primitive root thing works.
• Let's check our examples: for $p=7,n=4$, the only $(n-1)$-th powers are $\pm 1$, and we do see opposite columns matching. For $p=7,n=3$, columns $1,2,4$ and $3,5,6$ follow the same patterns respectively.
• Anyway, what we've shown above is that (returning to the original notation) $|S_a| = |S_b|$ if $\frac{a}b$ is an $(n-1)$-th power mod $p$.
• Great, so now we use the fact that there exists a primitive root $g$ with order $p-1$. $(n-1)$-th powers are just powers of $g^{n-1}$, which has order $\frac{p-1}{\gcd(n-1,p-1)}$.
• Relabel the columns $g^{\text{blah}}$, and columns with "blah" differing by multiples of $\gcd(n-1,p-1)$ have the same $|S_\bullet|$.
• Seems like we still care what the $|S_\bullet|$ are (adding an individual group isn't enough to be divisible by $p-1$): in the $p=7,n=4$ case, our three "groups" have values $4,4,7$, and we don't have $6|8$ or $6|14$.

Bijecting harder

• For what it's worth, the sum we're looking at is now $\frac1{\gcd(n-1,p-1)} \sum_{a = 1}^{\gcd(n-1,p-1)} |S_{g^a}|$. This is unhelpful when $\gcd(n-1,p-1)$ is large.
• Maybe we could look more carefully about how columns in the same group are related. From our $p=7$ cases it seems that they in fact take the same values (which is stronger than the multiplicities of the values being the same).
• Let's try to prove this: if we have $x^n + ax$ in some column, we want $y$ such that $y^n + ak^{n-1}y = x^n + ax$. Try $k^{n-1}y = x$? In general that only works if $p-1$ divides $n(n-1)$, which applies to both examples I looked at, so maybe it isn't true in general...
• Oh wait, it doesn't work for $p=5,n=3$. But even in this example, it seems we can say more than 
   "the multiplicities are the same".
• Let's return to how we proved that: essentially we used $(rx)^n + ar^{n-1}(rx) = r^n(x^n + ax)$. So the multiplicity of $b$ in column $c$ is the same as the multiplicity of $r^nb$ in column $r^{n-1}c$. Ha I bet we could just double count from here using the fact that $n,n-1$ are coprime or something.

At last, a solution

• Let $n_{b,c}$ be the number of times $b$ appears in column $c$. No, scratch that, we're taking powers and stuff so we want it to be the number of times $g^b$ appears in $g^c$ (we'll deal with $0$ separately). We can add $(n,n-1)$ to $(b,c)$ and this value remains the same. The number of times we have to do this to get back our original $(b,c)$ (working in mod $p-1$) is $\frac{p-1}{\gcd(n,n-1,p-1)} = p-1$, which is promising. So now we need to relate this to the original sum...ugh counting is hard.
• Let $f(d) = d-1$ if $d \ge 2$ and $0$ otherwise; we want to show the sum of all the $f(n_{b,c})$ is divisible by $p-1$. So by the above, we only need to account for the zeroes.
• Let's solve $x^n+ax = 0$. Other than $x=0$, we must have $x^{n-1} = -a$. This has $\gcd(n-1,p-1)$ nonzero roots for $\frac{p-1}{gcd(n-1,p-1)}$ nonzero values of $a$ and none for the rest (primitive root reasons). So we have $\frac{p-1}{gcd(n-1,p-1)}$ copies of $f(\gcd(n-1,p-1)+1)$ and some number of copies of $0$; this adds to $p-1$ as well, phew.

Time check: 2 hours 33 minutes (aaaaaaahhhhhhhhhh).

Problem 4

Find all functions $f:\mathbb Z \rightarrow \mathbb Z$ such that $f(x+y)((f(x)-f(y))^2 + f(xy)) = f(x^3) + f(y^3)$ for all integers $x,y$.

Some preliminaries

• We notice that $f(x) = x$ works thanks to the deep algebraic fact that $(x+y)(x^2-xy+y^2) = x^3+y^3$.
• Time to substitute stuff.
• $x=y=0$: $f(0)^2 = 2f(0)$, so $f(0) = 0$ or $2$.
• Putting $x=y$ makes the funny square term disappear, so let's do that: $f(2x)f(x^2) = 2f(x^3)$.
• $x=y=1$ gives $f(2)f(1)=2f(1)$, so $f(1)=0$ or $f(2)=2$.
• $y=0$: $f(x)(f(x)^2+f(0)) = f(x^3) + f(0)$. This seems like a useful way to get rid of $f(x^3)$.
• The FE is symmetric, so swapping stuff doesn't help.
• Oh, everything $=0$ is also a solution.

One solution ($f(x)=0$)

• Maybe assume $f(1)=0$. Then $f(x+1)(f(x)^2 + f(x)) = f(x^3)$. Putting $x=0$ gives $f(0)=0$. So we in fact have $f(x+1)f(x)(f(x)+1) = f(x)^3$. This lets us induct downwards ($f(x+1) = 0$ implies $f(x)=0$, so $f(x)=0$ for all $x\le 1$. Then do $y=-1$? $f(x-1)(\cdots) = f(x)^3$, so we can also induct upwards. Cool.

One annoying solution (something something parity)

• So we're left with $f(1)\ne0$, so $f(2)=2$, however useful that may be.
• Maybe $f(a)=0$ for general $a\ne 0$ gives the same conclusion...no, I think above we used $1^3=1$.
• I just wrote something wrong because there was a typo in one of the above lines which I have now fixed.
• Maybe we can try to get rid of the $f(0)=2$ case. Put $x=0,y=2$: $4=f(8)+2$, so $f(8)=2$. $x=y=2$ gives $f(4) = \pm 2$. Omg everything $=2$ is also a solution. Ok yes, now I have all the possible constant solutions (really should have checked that first).
• Anyway. Suppose $f(0)=2$, then $y=0$ gives $f(x)(f(x)^2 - 4f(x) + 6) = f(x^3)+2$. Put $x=1$. We know $f(1)=2$ should work so we can factor that out: $(f(1)-2)(f(1)-1)^2 = 0$. Likewise for $f(-1)$.
• Let's put $y=1$. In the $f(1)=1$ case, we have $f(x+1)(f(x)^2-f(x)+1) = f(x^3)+1 =f(x)(f(x)^2 - 4f(x) + 6) -1$. This gives us some sort of inductive statement. If $f(x)=2$ then this gives $3f(x+1) = 4-1=3$ so $f(x+1)=1$. If $f(x)=1$ then we get $f(x+1) = 3-1=2$ so $f(x) = 1$ for odd positive $x$ and $2$ for even positive $x$ omg please don't tell me there's another solution.
• We also have $f(-1) = 1$ or $2$, and $f(-1)=2$ implies $f(0) = 1$, contradiction, so $f(-1)=1$. Now $y=-1$ gives $f(x-1)(f(x)^2-f(x)+1) = f(x^3)+1 =f(x)(f(x)^2 - 4f(x) + 6) -1$ so we can induct downwards as well (this looks a lot like how we dealt with the $f(1)=0$ case...) and get $f(x)=1$ for odd $x$, $2$ for even $x$. Great we have to check this. The $x,y$ same parity cases are clear. The last is $1(1^2 + 2) = 1 + 2$.
• Please no more cases.

The other constant solution ($f(x)=2$)

• We are left with $f(1)=f(0)=f(-1)=2$ (if $f(-1)=1$, reasoning as above gives $f(1)=1$, I think) and $f(0)=0$ cases. Let's do the first one.
• We've been fairly successful with just plugging $y=1$. Doing that gives $f(x+1)(f(x)^2-3f(x)+4) = f(x^3) + 2 = f(x)(f(x)^2 - 4f(x) + 6)$. Aha. Induction time. Putting $f(x)=2$ gives $2f(x+1) = 4$, so $f(x+1)=2$. Repeat with $y=-1$ to induct downwards, so we get the constant solution $f=2$.

The final solution ($f(x)=x$)

• At long last, we're left with $f(0)=0$ (and also $f(2)=2$ if that ever turns out to be useful). $y=0$ gives $f(x)^3 = f(x^3)$, so $f(1) = 0$ or $\pm 1$. Oh wait we ruled out the $0$ case earlier. Wait $f(x)=-x$ isn't a solution right? I don't think it is.
• If $f(1)=-1$, then $f(x+1)(f(x)^2 + 3f(x) + 1) = f(x)^3 - 1$. So $11f(3) = 7$ contradiction? I really hope I haven't made some arithmetic error - typing working instead of writing is harder than I expected for this sort of question.
• If $f(1)=1$, then $f(x+1)(f(x)^2-f(x)+1) = f(x)^3+1$. Put $x=2$, $3f(3) = 9$ so $f(3)=3$. Ok please let induction work. If $f(x)=x$, then $f(x+1) = \frac{x^3+1}{x^2-x+1} =x+1$ phew. So we're left with the negative case. 
• If $f(-1)=1$, then $x=2,y=-1$ gives $1(1^2 + f(-2)) = 8 + 1$ so $f(-2) = 8$. Then $x=y=-1$ gives $8=2$, contradiction.
• So $f(-1)=-1$, and then I'm fairly certain putting $y=-1$ lets you induct downwards and we at last get the last solution $f(x)=x$.

Time check: 3 hours 42 minutes (oh no oh no oh no oh no)

Problem 5

Determine all real numbers $x$ between $0$ and $180$ such that it is possible to partition an equilateral triangle into finitely many triangles, each of which an angle of $x^\circ$

Initial guesses

• Time to draw pictures.
• It's kind of annoying that they're asking for real numbers, not say integers.
• Ok, so an obvious thing to do is to divide the triangle into congruent pieces:

Some primary school math.

• So $x=30,60,90,120$ work.
• But surely using only congruent triangles is restricting too much. We could...oh. We could do this:

Cake slicing, yum.

• ...which lets us get anything of the form $\frac{120}n$ or $\frac{90}n$. Or $\frac{60}n$ if we radiate from a corner but we've already covered that case.
• That makes quite a funny solution set...can we get like $\frac{180}n$ in general or something? Wait is that already covered in the previous cases? No, $36$ doesn't work. Hmm.
• Oh, we can move the radial point, then anything that divides the gcd of the three angles in the centre works. I should rephrase that, since gcds of real numbers are not things in general. Anything that divides the three angles at the centre. Oh that means that it has to divide $360$.

Less fair cake slicing.

• So presumably any $\frac{360}n$ could work (except $x=180$, of course), as long as we can get the angles in the centre to cooperate. Is that true? Yeah, you just pick two obtuse multiples of your desired angle and intersect two circles.

Trying to prove it

• That seems like a reasonable solution set, so why does nothing else work? Partitions of a triangle into triangles can get arbitrarily weird looking...
• Ok, let's pick some random angle $\theta$ and try to draw something. So maybe an angle $\theta$ here, and there...
• Right, so we are basically picking two sides and saying "these differ by $\theta$". And having a chain of them forces all of their relative gradients.
• So if we draw a graph where we join edges which are $x$ apart, then...ok in our general construction we get a nice cycle. And a cycle would force something like $nx=360$?
• Wait, no. We'd need some nonsense like directed graphs because lines can "go back". Time to draw pictures of that case.

More pictures

• We could plausibly end up with something like:

Some people don't get frosting.

• As the horizontal line moves, $x$ would vary - something like everything below $60$ would work?
• But then blocking off a trapezium leaves us with...the same thing again, which isn't exactly right. But it does seem to suggest that something more intelligent than "divide radially like a cake" would give a larger set of solutions.

Oops

• Oh no, I've hit 4 hours. Maybe I'll try this problem again the next time I have to write a post.

Post mortem

Problem 1

So it's clear that the main idea turned out to be homothety. How did I get there? I think the crucial step was trying to move $Q$ while fixing $P$ and trying to visualise how $S$ moved (if you think about it, it moves along the perpendicular bisector of $AP$, which intersects with $AO$ at a unique point). I probably think this way because I like to bash, but it tends to be useful to see how points are related (imagine you're drawing the diagram on geogebra and get to move the blue points around - where do the black points go?)

Other things to consider: trying to relate weirder points (e.g. $M$) with points you're more familiar with, though this was less useful in this context, in part because the funny conditions made it more of an "applying basic principles" sort of question rather than a "recognising configurations" sort of question.

Problem 2

Reading back what I wrote, I realise I was being an absolute potato: the number of L shapes should just be $a+1011$, which gives you a contradiction when considering white minus black mod $4$, as I attempted to do. I think my reasoning up to that point is sound: first, you determine what property of $2022$ is relevant for this question. (Would it work for all integers? All even numbers? All multiples of $6$ more than $1998$?) Then using this information, you realise that you want to colour because your answer depends on parity (well, actually mod $4$), and the standard colouring for L tiles is stripes (checkerboard doesn't work because it'd cover two of each colour).

I suppose the lesson to be learnt from the (far less elegant) solution that came after that mistake is: when a smart colouring fails, doing something more general and brute-forcing simultaneous equations will result in an answer (see also: Sheldon solving IMO 2016 P2 with 9 simultaneous equations).

My comment about looking at the enclosed area was a reference to this problem.

Problem 3

A recurring theme in everything I wrote for this is: try small cases, make hypotheses, try to prove hypotheses, and if the proof doesn't go through use it to find a counterexample. Also, it's gratifying that my initial intuition about double counting was correct. Why did I think of that? I think I imagined values of $x^3+ax$ being arranged in tables from the beginning; the question cared about columns and so the natural thing to do would be to look at rows. As it so happened, the rows were very well-behaved.

Problem 4

So that was long and horrible. The main idea is: the $f(x^3)$ term is gross but substituting $y=0,\pm1$ and comparing leaves us with only the basic $f(x)$ terms as well as one copy of $f(x\pm1)$; that and the fact that the question is on integers should lead one to suspect induction. After that, it's a matter of case bashing and plugging in the different possible fixed values. Also, not failing arithmetic (I really hope I didn't fail arithmetic.)

As I noted repeatedly, I really should have checked for obvious families of solutions (especially the constants) - that would have prevented me from finding contradictions where there were none to be had.

Problem 5

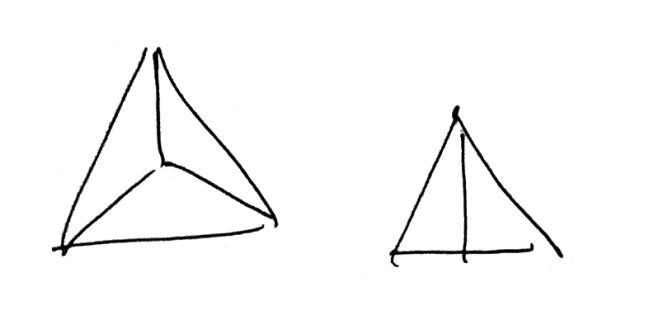
Well I can't comment since I haven't solved it (yet?) but I'm fairly certain my guess of $\frac{360}n$ is wrong lol.