Elliptic Curves v2.0

(Dylan here) In January, Zhao Yu wrote a piece about elliptic curves. To prioritise the various remarkable consequences that follow from the theory, many things were black-boxed. Today, I would like to open the box. I expect to make a mess and not clean it up; I hope you are okay with that! 

But first, some personal tales.

Qn. Is (olympiad) maths actually useful?

I've wrestled with this question for a long long time; it would be comforting to know that what I'm passionate about and invest a lot of time and effort into is also objectively meaningful. While I don't yet have a complete answer, here are my thoughts thus far. 

First, I acknowledge the open-endedness and vagueness of the question as posed. What is (or isn't) mathematics? Does the answer vary between different types of mathematics (e.g. pure/applied, high school/undergraduate/research)? What does useful mean, and is there an objective aspect?

Of course, fuzzy terms and open interpretations doesn't stop us from asking such questions and trying to answer them anyway! For example, we intuitively work with dimensions and limits years before we formalise the notions in axiomatic rigour. We ask questions like "how fast does this algorithm run?" or "is this sequence chaotic and random, or rigid and structural?" with the same air of ambiguity. Yet we find ways to reasonably, rigorously answer them. Furthermore, we can accept multiple interpretations (e.g. an algorithm can have a vastly different worst-case runtime from average run-time) without contradiction. 

Back to the question, we first list common positive answers. Maths is the language of the natural world, in the sense that seemingly magical physical phenomena may be explained by mathematical models. This is true both at the fundamental level (e.g. particle physics, gravity, electricity) and at the empirical level (e.g. weather forecasts, electronics, social diversity). Specific modern areas in which maths knowledge is highly valued are market predictions (finance), machine learning (computing), and precision design (engineering). Indirectly, maths encourages pattern recognition and abstraction, rational and critical thinking, and meticulousness, valuable qualities for many technical positions. There is also a strong association of mathematics with general intelligence (the ability to learn, absorb, and process information). And the patterns and structures in maths are innately beautiful, as they exist largely independently of our personal experiences. 

Now for common negative answers. Maths neglects the emotional, social, and cultural aspects of a well-rounded education. There is low emphasis on understanding irrational behaviour (which is a big part of being human, thus more useful to study). Applications are concretely more impactful (e.g. saving lives, building houses, protecting the environment) and should drive theory (instead of studying maths independent of downstream applications). Maths wrongly encourages the idea that there is only one right answer, and that there are fixed methods to finding answers. Intelligence is not the most crucial ingredient of a meaningful life.

Now let's specialise the question to: is olympiad maths useful for high school students? Well, it depends. In the period of exposure to various aspects of the world and growing in maturity, maths is certainly important for reasons described above. But also other subjects are just as important, with ideas not captured by maths, as described above. Specifically (and in my personal opinion), the value of olympiad mathematics is the exposure to so many new ideas, examples, and concepts that we wouldn't otherwise encounter in real life. Think of someone who can perceive infrared in addition to the visible spectrum; the maths-educated similarly have added perspective. 

But then what is the difference between mathematics and other areas of study (e.g. medicine, psychology), which also forge new lenses through which one perceives the world? I would say the key difference is that mathematics also develops the meta. By which I mean thinking about thinking, or thinking about thinking about thinking, or so on. Like simple vs. compound interest, but in multiple layers (like in idle games). Critically, the human intuition we have naturally, accumulatedly built up since we were babies only lie in the "first meta-level"; to go beyond human intuition and grow higher meta-levels (e.g. learning about how we learn), we have to learn to be comfortable with the abstract and foreign (e.g. "what if I lived in 7 dimensions?").

In short, maths makes one a better thinker in the meta sense, such as by introducing more ways to think (e.g. "this is water") and more questions to ask ("what is water?"). This is a slice of my current (vague and incomplete) answer; it hinges on many unstated assumptions and interpretations (many of which I probably am not even consciously aware of), so I expect disagreement (and I'd be interested to hear your thoughts too). Hope it was insightful anyway, and got you thinking about whether/how mathematics is useful to you. 

Time for maths!

Elliptic Curves v2.0

This is not an olympiad maths post, but an exposure post. I will try to prioritise motivation of ideas at some intermediate level of accessibility (don't worry if you feel absolutely lost in the abstraction; you can always come back to this again). I will ask questions in square brackets [why?] which I feel are worth asking (and if you have the time, pausing to think about); some of them will eventually be answered, but I truly believe the questions are more important than the answers. 

0. Spoilers

Zhao Yu's article is linked here; I would like to summarise some key elements. But this is also akin to a spoiler; in some sense, the answer is told to you before the question. So here's a spoiler warning; you may wish to skip this subsection and return to it after. But if you don't want to think so much, just read on (no guilt required). 

Okay, summary time.

• An elliptic curve has both algebraic structure (given by a polynomial equation; notion of degree) and analytic structure (a geometric torus/quotient of the complex plane; notion of dimension). In addition, it has an abelian group law (i.e. a "zero" point, and a way to add/subtract points). [Do we already know of other such spaces?]
• The group law is a way to generate new points on the curve from existing ones. The fact that the group operation is given by rational-coefficient polynomials also means that rational points on the elliptic curve are stable under the group law (i.e. adding two rational points gives a rational point). This gives a solution to the fruit meme: begin with a small rational solution (but involves negatives, so not allowed), then keep adding it to itself until it becomes a positive solution. 
• Elliptic curves have a relationship with elliptic integrals (i.e. integrals that you might get if you try to compute the perimeter of an ellipse). This perspective is no longer necessary in the modern treatment of elliptic curves, but it was important in the historical development of the theory. I will also not say more (since it does require some confidence in calculus to engage with).
• Elliptic curves have connections with number theory. Allow me to draw an analogy to the Riemann zeta function $\zeta(s) = \sum_{n\in \mathbb N} n^{-s}$, a special function over the complex plane, which has both analytic (i.e. calculus-able) and number-theoretic (i.e. factorisable-by-primes) properties. Similarly, the $j$-function is a special function over the upper-half complex plane, satisfying a specific set of symmetries, which grants it both analytic and number-theoretic properties as well. It turns out that perhaps the natural domain of the $j$-function shouldn't be "the upper-half complex plane", but "elliptic curves"; the set of elliptic curves (a very very abstract set) is naturally identifiable with (a quotient of) the upper-half complex plane. Everything in this paragraph is highly abstract and should just be ignored.

Okay, now please pretend you don't know anything about elliptic curves; in fact, forget for a moment that the very concept of an elliptic curve ever existed. We'll try to chance upon it ourselves.

1. Background

To set the stage, we first review slices of algebra and geometry separately. Because this is a finite blog post, I will cherrypick and be brief on some things, while elaborating more on other ideas which will eventually be relevant. 

1.1. Algebra

1. We first encounter algebra in school as a tool to extract mathematics from a paragraph of information. For instance, the system $a+b=30, 2a+4b = 100$. [Can you think of a word problem corresponding to this system?] [Why is there only one solution?
2. We also encounter non-linear equations such as $x^2+x=12$, perhaps related to "a rectangle of area $12$ whose side lengths differ by $1$". [Can you see the distributivity law encoded here?] [Why do we reject the negative solution $x=-4$? Do `unphysical' solutions still have use in, say, intermediate steps?]
3. Other (Diophantine) equations such as $2x+3y=1$, $a^2+b^2=c^2$, and $w^4=z^4-1$. They may be solved over the integers: $(x,y) = (-1+3t,1-2t)$ (Bezout's and CRT), $(a,b,c) = k(m^2-n^2,2mn,m^2+n^2)$ (Pythagorean triples), and $(w,z) = (0,\pm 1)$. But they could also be solved over the rationals, reals, complex numbers, integers modulo $5$, rational-coefficient polynomials, real power series, etc. [What are properties of a general space $R$ for which such polynomial equations make sense, and can be solved over?]
4. Algebraic identities, such as the $2$-square identity $(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(ad+bc)^2$ and Sophie Germain's identity $a^4+4b^4 = (a^2+2ab+2b^2)(a^2-2ab+2b^2)$. [What are properties of a general space $R$ for which such identities hold true?]
5. Symmetries of polygons and polyhedra; the Gaussian integers $\mathbb Z[i]$, or the space $\mathbb Z[\varphi]$ in which Fibonacci numbers "naturally live" (see my previous post); lattices in the plane (discussions for another day). 

One may use points 3 and 4 to motivate an (intuitive, but entirely formalisable) definition of a (commutative unital) ring $R$ which has operations $+,-,\times$, special elements $0,1$, and obeys various rules (e.g. commutativity, associativity, distributivity). These rules, or axioms, are shared properties of the various familiar spaces listed in point 3 above; they now become characterising properties for our general object. [Can you try to formulate the axioms on your own? Can you give other examples of rings not mentioned above?]

1.2. Geometry

1. Euclidean (planar/2d) geometry: lines, circles, ruler-compass constructions. [Why can't we construct $\sqrt[3] 2$ or $20^\circ$ using a straightedge and compass? Is there a conflict between the continuous/analytic nature of the real line, and the discreteness/rigidity of ruler-compass constructions?]
2. Some remarkable results: (a) Pappus' theorem "$2$ lines, $3$ points on each line, draw the $3$ crosses, the $3$ intersections are collinear". It's amazing that such a non-trivial result arises from straight lines alone (no compass needed!). (b) Pascal's theorem "$6$ points on a circle, draw the $3$ crosses, the $3$ intersections are collinear". [Why do their statements look so similar? What does two lines have to do with a circle?]
3. Geometric transformations: rotation, dilation, reflection, inversion, (skewed) scaling, shear, projection. 
4. 3d geometry: that the surface area of a sphere and its bounding cylinder are equal, but volumes are in the ratio $2:3$; or a result/observation by Eudoxus that "the intersection of a sphere with a cylinder tangent to the sphere, is a figure-eight loop traced out by a composition of two rotations". [Can you prove it?] This result falls in the meta-picture of "problem = constraints, solution = parameterisation"; one may wish to draw a meta-link with the problem-solution pairs listed in point 3 of algebra. 
5. (Cartesian) coordinates: now every theorem in geometry has an algebraic proof! [Does that mean geometric results have algebraic meaning?] Also, objects now have a notion of degree (e.g. a line/plane has degree $1$, a circle/ellipse degree $2$, based on the associated polynomial) and dimension (intuitively, the number of coordinates required to parameterise the object).
6. Projective geometry: imagine a painting of train tracks; the tracks are parallel in real life, but meet at a point on the horizon on the picture. One may understand the projective plane as gluing on a "line at infinity" (or if you prefer, a "circle of infinite radius" at infinity) at which parallel lines meet. One may also opt for the view that the projective plane is the set of lines in 3d through the origin: if you think of the plane (the ground on which the train tracks lie) as $z=-1$, and place the painter/eye/observer at the origin, each point on the plane then corresponds to a unique "line-of-sight" through the origin, but there are also lines through the origin parallel to the plane (corresponding to the horizon line, i.e. line at infinity).  
   
7. Alternative coordinates; embedded geometry (e.g. knot theory); spherical/hyperbolic geometry; general surfaces, manifolds, bundles (discussions for another day). 

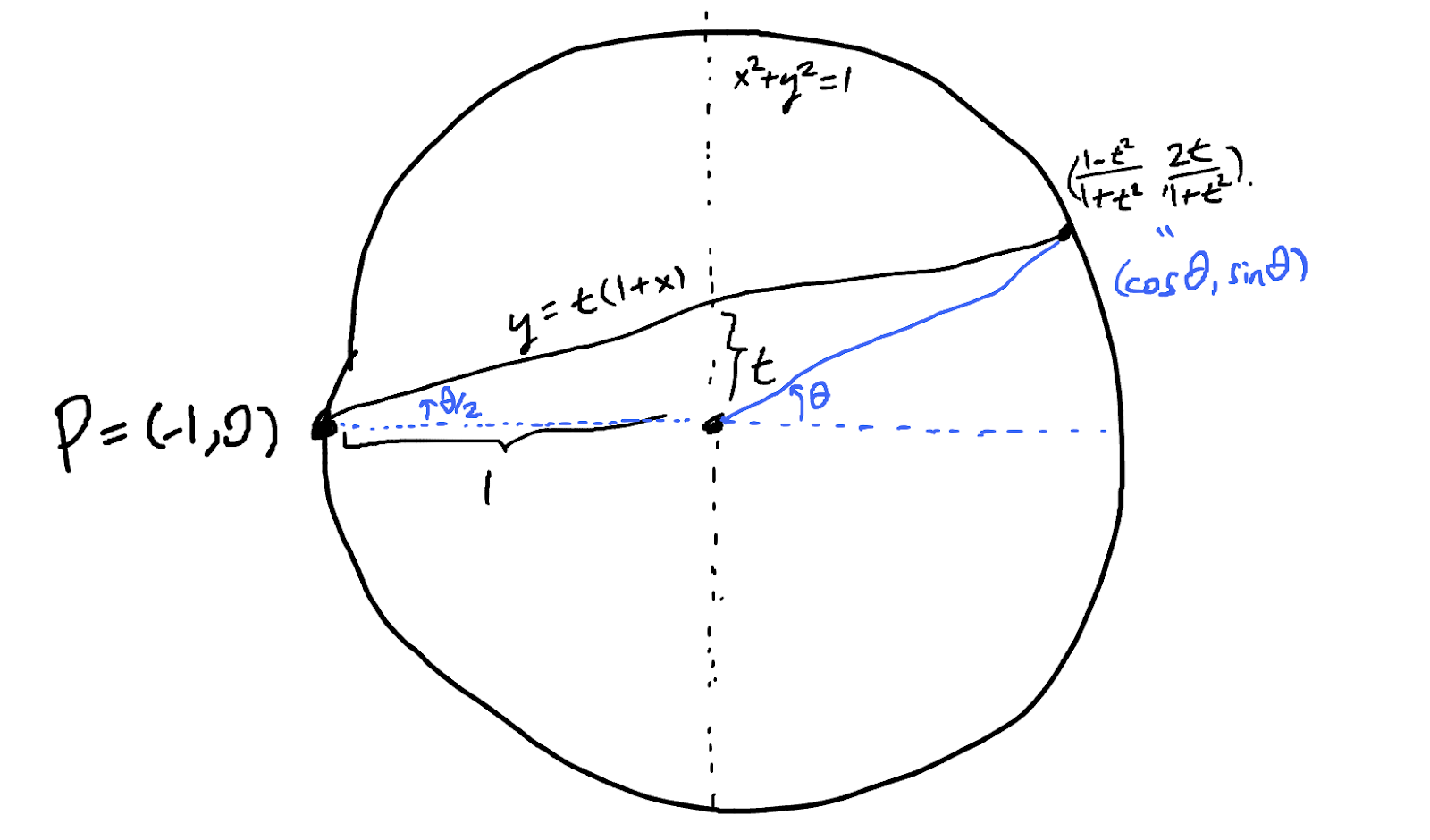
2. The unit circle

We see that a natural region of overlap between algebra and geometry is in the zero locus of polynomials. Polynomial equations can be solved purely algebraically, perhaps even over discrete spaces such as the integers/rationals, but they can also be viewed as cutting out curves/surfaces! We would like to investigate more.

Let's try an study one such object: the unit circle $S^1 = \{(x,y): x^2+y^2=1\}$.

Now, I want to understand the unit circle over various spaces (e.g. $R=$integers, rationals, reals, complex numbers, integers modulo $5$, rational/real-coefficient polynomials). So, let's update the notion to specify what underlying space we are working with:

$$S^1(R) = \{(x,y)\in R^2: x^2+y^2=1\}$$ 

Let's try to understand the unit circle over some familiar spaces.

2.1. $S^1(\mathbb R)$

First up, our favourite space $R=\mathbb R$, the reals. It's so nice that we can draw a picture reflecting its geometry! And, we learn at school that one may parameterise points on the circle by trigonometric functions of an angle: 

$$S^1(\mathbb R) = \{(\cos \theta, \sin\theta) : \theta\in \R/2\pi \Z\}$$

where $\theta\in \R/2\pi \Z$ means that the angle $\theta$ is a real number determined up to integer multiples of $2\pi$. 

It is not ideal that the solution is not expressed in a polynomial-ish manner (the trigonometric functions are power series, very analytic in nature). A bit of optimism here pays off: we get a second parameterisation,

$$S^1(\mathbb R) =\left \{(\frac{1-t^2}{1+t^2}, \frac{2t}{1+t^2}) : t\in \R\cup \{\infty\}\right\}$$

This is obtained by picking one's favourite point on the circle (in this case, $P = (-1,0)$), drawing a line of gradient $t$ through $P$, and computing the coordinates for the second intersection. One may also prefer to understand it as inversion about $P$, or projection to the $y$-axis with respect to $P$, or that $t$ is the tangent-half-angle. 

[Do these two parameterisations extend to parameterisations of $S^1(\mathbb C)$? How about the picture?]

Apart from the two explicit parameterisations, there is also a third geometric interpretation:

$$S^1(\mathbb R) = \{\text{rotations of the plane about the origin}\}$$

This interplays with the angle parameterisation nicely: if special "zero" point $O = (1,0)$ is fixed ($\theta(O) = 0$), and any other point $P$ on the unit circle is identified with the unique rotation sending $O\mapsto P$, then composition of rotations corresponds to addition of angles! In particular, there is an abelian group law (i.e. an addition law; "abelian" means commutative, i.e. addition may be performed in any order) on $S^1(\mathbb R)$. 

But it's not as if the angle parameterisation is "more natural" than the $t$-parameterisation in any objective sense (or other parameterisations, e.g. take a favourite point different from $(-1,0)$; or $4$ local projection parameterisations $(x,\pm \sqrt{1-x^2}), (\pm \sqrt{1-y^2},y)$ that glue together to parameterise the whole circle). So, let's take a look at how the group law acts on the parameter $t$: 

$$t_{P\oplus Q} = \frac{t_P+t_Q}{1-t_Pt_Q}$$

Brilliant: it acts polynomial-ishly! You might also recognise the tangent addition formula here. 

2.2. Generalising the group law

Let's now see if the group law on $S^1(\mathbb R)$ can be generalised to $S^1(R)$ for general rings $R$. We don't expect nice parameterisations in general, but we can always work with the original expression for points on $S^1$: as a pair of coordinates!

$$(x_1,y_1) \oplus (x_2,y_2) = (x_1x_2-y_1y_2,x_1y_2+x_2y_1)$$

One way this can be motivated is by using the angle parameterisation, and applying trigonometric addition formulae. The fact that the group law is given by polynomials means that it has a good chance of generalising to over arbitrary rings $R$! We (more specifically, you) may now get our hands dirty and try to prove that the group law is (a) well-defined (i.e. the RHS is in fact a point on $S^1$), (b) commutative, (c) associative, and (d) has identity $O = (1,0)$ with inverses $-(x,y) = (x,-y)$. 

Okay, but what does the group law really mean? Did we just get lucky?

Let's try to understand the group law from an algebraic perspective. There is similarity to the $2$-square identity described earlier! In fact, this group law is more natural by working in an enlarged ring $R[I]$ adding an element $I$ that squares to $-1$: 

$$(x_1+y_1I)(x_2+y_2I) = (x_1x_2-y_1y_2) + (x_1y_2+x_2y_1)I$$

(Here, I used a capital $I$ because it needs to live outside the ring $R$. For example, if $R=\mathbb C$, the added element $I$ is different from the elements $\pm i\in \mathbb C$.) This hints at the powerful idea that results about a particular space may be understood much more naturally in an extension of the space (and working in such an extension is often unavoidable for proofs). 

Now let's try to understand it geometrically. Fixing a "zero" point $O$, if I wished to add two points $P,Q$ on the circle, what I would do geometrically is:

1. Draw the line $PQ$.
2. Draw the line through $O$ parallel to $PQ$.
3. This line intersects the circle at a second point $P\oplus Q$.

Drawing a parallel line is something pretty specific to Euclidean geometry; in our more general language of projective geometry, the procedure is:

1. Draw the line $PQ$; it intersects the line at infinity at some point $R$.
2. Draw the line $OR$; it intersects the circle at a second point $P\oplus Q$.

Now what does it geometrically mean for the addition operation $\oplus$ to be associative? Let's draw out the computation of $(P\oplus Q)\oplus R$ and $P\oplus (Q\oplus R)$ (where the line at infinity is brought into the picture as just a regular line): 

Now, the fact that $(P\oplus Q)\oplus R=P\oplus (Q\oplus R)$ is just Pascal's theorem! 

What does this mean? Well, I alluded earlier to the fact that geometric results may have algebraic meaning. So, one may say that "Pascal's theorem encodes the associativity of the group law on the unit circle". 

[It turns out that Pappus' theorem encodes commutativity of ring multiplication! Are you brave enough to try to make sense of Pappus' diagram in a non-commutative ring e.g. quarternions $\mathbb H$, and demonstrate its failure?]

2.3. $S^1(\mathbb F_p)$ and others

This last bit of exploration is not too relevant to elliptic curves, but I feel the discussion of the unit circle would be incomplete without it. Let's try to understand $S^1(\text{integers mod }p)$. How many points does it have? What is its group structure?

For example, $S^1(\text{integers mod }11)$ has $12$ elements, given by $(0,1)$ and $(5,3)$ (with the usual freedom of signs $\pm$ and swapping $x\leftrightarrow y$). They have orders $4$ and $3$ respectively, so the unit circle is the cyclic group of order $12$. 

More computations show that $S^1(\text{integers mod }p)$ has size $p\pm 1$ (whichever is divisible by $4$), and is always cyclic. [Try to prove this! Does this have anything to do with the fact that $S^1(\mathbb R)$ is "$1$-dimensional"?]

[What is $S^1(\mathbb Q[X])$, the unit circle over rational-coefficient polynomials? How about $S^1(\mathbb Q(X))$, the unit circle over rational-coefficient polynomial fractions?]

Finally, an subtle but important meta-remark is that the unit circle is not just a separate group for each ring; related rings have related unit circles. For example, the fact that $\mathbb Q$ sits in $\mathbb R$ means that $S^1(\mathbb Q)$ also sits in $S^1(\mathbb R)$. One may formalise this in the following sense: $S^1$ is a meta-map $\{\text{rings}\}\to \{\text{abelian groups}\}$ such that if $R\to \tilde R$ is a map respecting the ring operations, then it (naturally, uniquely) induces a map $S^1(R)\to S^1(\tilde R)$ respecting the group operation. Such a meta-map is called a functor.

3. What does all this have to do with elliptic curves?

Earlier, I asked about why Pappus' and Pascal's theorem are so similar in configuration; in particular, what does two lines have to do with a circle. The answer is that they are both conics (i.e. cut out by degree-$2$ polynomials)! [Why can two lines be cut out by a degree-$2$ polynomial?] The optimist would then try to see if Pascal's theorem generalises to $6$ points on any conic (i.e. degree-$2$ plane curve, e.g. ellipse/parabola/hyperbola). The answer is yes! [Can you already see it to be true for an ellipse? Think of what transformations you can do to the plane!] 

Well, actually the $3$ lines in Pappus' theorem (the $2$ initial lines, plus the final line of collinearity) are rather symmetric in nature. So perhaps the right question was: what does three lines have to do with a line and a circle? The answer: they are both cubics (i.e. cut out by degree-$3$ polynomials)!

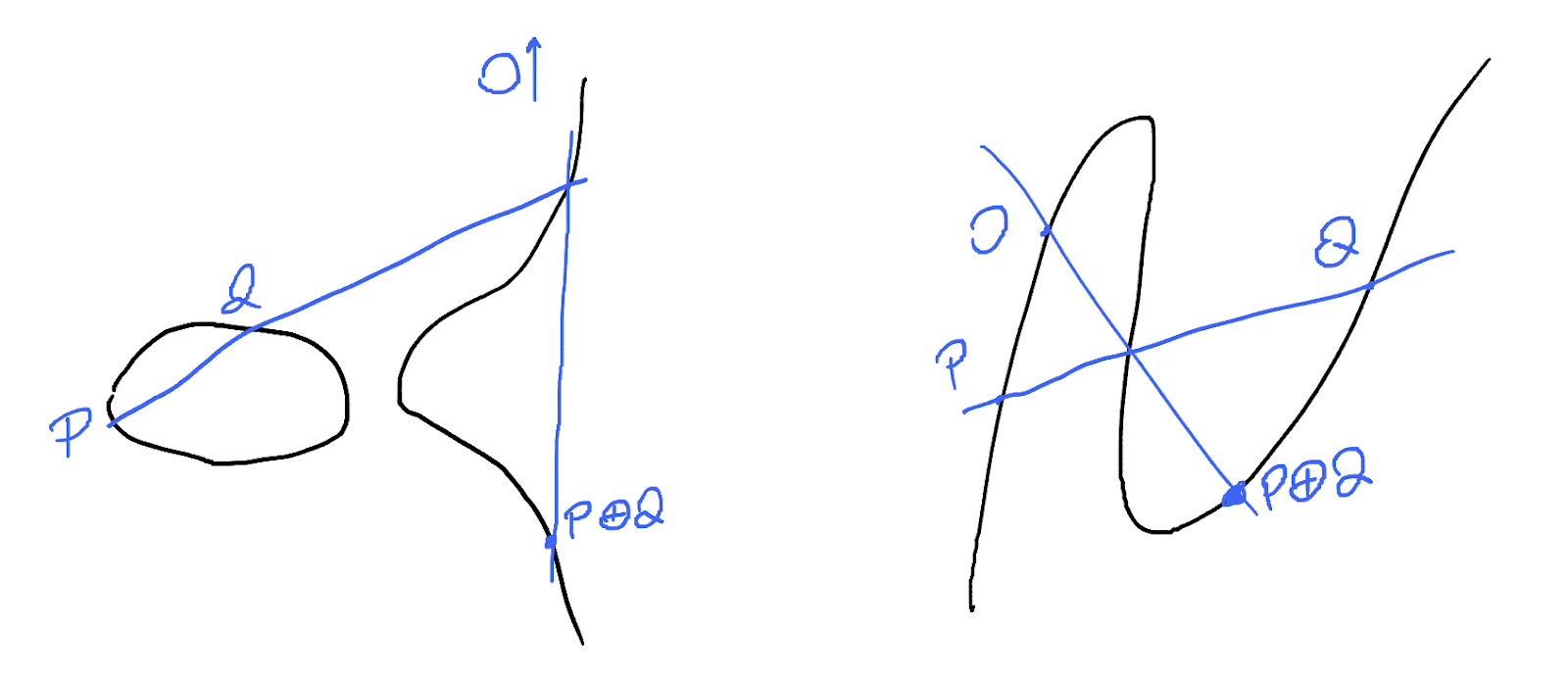
Now that we know the group law on the unit circle, let's try to generalise it to define a group law on a general cubic: 

1. Fix a "zero" point $O$ on the cubic.
2. Given two points $P,Q$, draw the line $PQ$; it intersects the cubic at a third point $R$.
3. Draw the line $OR$; it intersects the cubic at a third point $P\oplus Q$. 

To show this is associative, it suffices to prove the generalisation of Pappus'/Pascal's theorem to cubics, known as the grid theorem. [Can you state it?] One could of course bash out a coordinate proof by hand (using Vieta to express the coordinates of the third intersection point of a line and the cubic, given the coordinates of the other two), and then either give up or use a computer algebra system to do the bashing for you instead. One may wish for a "synthetic proof", but cubics are not even ruler-compass friendly. But perhaps plotting enough pictures on geogebra is sufficient for you to believe that is true (and wait for a "nice" proof in the future; perhaps you have also been waiting for a "nice" proof of Pascal's). 

[In fact, the Pappus configuration is formed by $3$ sets of $3$ lines; does this mean it can be generalised to a statement about $3$ cubics?]

4. Conclusion

Okay, so that is my attempt of explaining why cubics have a natural group law: by trying to motivate it as a generalisation of the all-familiar group law of rotations on the unit circle. With regards to the complex torus perspective, I think it can wait for the future (when you learn about/are exposed to the beauty of calculus over the complex numbers; the eager may wish to first think about and try to understand $S^1(\mathbb C)$). If this piece inspired some questions of your own that I didn't get to ask, I would love to know!

Now let's put on a critical hat. I think I only answered the question of why one might hope a group law exists (as a generalisation of Pappus'/Pascal's theorems), but not really why we would expect the generalisation to work (after all, most dreams stay as dreams). I even swept under the rug that the line at infinity could be moved to a usual line (not at infinity); it might even worry you that the line at infinity doesn't intersect the circle, but the collinear line in the Pascal configuration (as drawn above) does. [Is this a problem with our underlying space, the real plane $\mathbb R^2$?] And Pascal's theorem itself doesn't have a simple synthetic proof (I've seen various proofs over the years, including one 3d proof, but I remember none of them!), so this just piles on more mystery! And how about the hyperbolic tangent addition formula? Does that have algebraic/geometric meaning as well?

If you share my sentiments of the previous paragraph, I would like to offer some reassurance: if you consider the above motivation as "geometric", there is in fact a more natural "algebraic" reason for why the group law exists. General algebraic sets (i.e. spaces cut out by polynomial equations) in fact have rich natural structures living on them, which in the special case of a plane cubic, "happens to reduce to" a group law. Unfortunately, these structures are highly abstract, and take a long time (~2 years, including learning things that are not directly content-relevant but very much idea-relevant) to even set up and understand. Fortunately, you are still young and energetic (considering you read this far), so this is very much in reach if it is something that interests you! 

On a complete tangent, writing this blog post reminded me that back in the days, Zhao Yu and I participated in the PuMaC '15 Power Round, which was about elliptic curves. I have long forgotten my experience of it back then, but I'm sure it had some unconscious effect on us. The PuMaC Power Round is one (of several) entrypoints into engaging with undergraduate mathematics at the high school level. For convenience, here are the past year Power Round topics (listing in case any of it interests you): algebraic geometry (’23), PID structure theorem (’22), mixed volumes and convex bodies (’21), billiards and ant-paths (’20), extremal graph theory (’19), combinatorial game theory (’18), Lie algebras (’17), pseudorandomness and cryptography (’16), elliptic curves (’15), four-square theorem (’14), knot theory (’13), algebraic numbers and diophantine approximation (’12), projective and perspective geometry (’11), graph minors and four-colour theorem (’10), lattice theory (’09), quadratic forms (’08), lattices (’07).

Happy mathing!