Another win for three dimensions

(This is David.) I'm back with a short post about a beautiful proof for a beautiful problem I saw recently.

Three dimensions?

Let me explain the title. I think it was during a decent IMO where Grant Sanderson (of 3blue1brown fame) gave a talk about problems that are super easy once we move to a higher dimension. If you weren't there at the talk, he also made it into a youtube video - I highly recommend watching it if you haven't already!

Here at the SIMO X-Men blog, we aren't unfamilliar with this idea - one of the most popular blogposts to date is Glen's Spacetime, Special Relativity, and a Lot of Circles where we saw that interpreting circles as points in 3-dimensional space was a really powerful tool for lots of geometry problems involving tangent circles.

And the nice thing is, this trick doesn't stop at puzzles and Olympiad problems - it also shows up in real research. Arguably, the recent breakthrough for the sofa problem used this idea, and I've also seen it used in other papers. I wrote about one example in this blogpost where an optimization problem was solved by, once again, considering it as a slice of a higher-dimensional problem.

So, here's another problem that can be done in this way!

The problem

Suppose that a set $S$ of points in the plane is given, where no three points are collinear and no four points are concyclic. Show that there exists a unique triangulation of the convex hull of $S$ where the circumcircle of each triangle doesn't contain any point of $S$ inside of it.

This problem is famous and has a name: the Delaunay triangulation.

Some whitespace to follow, in case you want to try the problem yourself.

...

...

...

...

...

How you might solve it

It turns out that there's a not-too-difficult way to go about this problem, and the key is to focus on what happens for a quadrilateral. I'll just leave this image here:

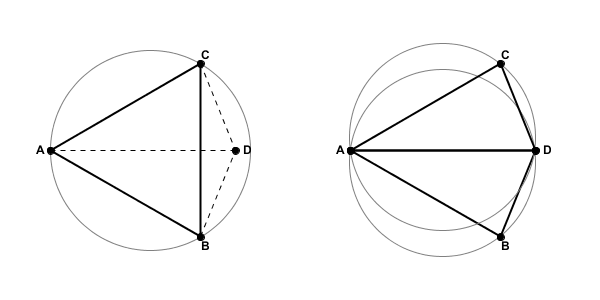
The amazing solution

So the above solution will work, but here's one for "the book" that really makes things obvious (which I learnt from this math.SE post):

Lift each point $(x,y)$ to the paraboloid $\{(x,y,z): z = x^2 + y^2\}$ (i.e. draw a vertical line and move each point up to the surface of the paraboloid). Then, note that:

Circles get lifted to planar sections of the paraboloid.

This is easy to see from coordinates: a circle is $(x-a)^2 + (y-b)^2 = r^2$, but $$\begin{align*} (x-a)^2 + (y-b)^2 - r^2 &= (x^2 + y^2) - 2ax - 2by + (a^2 + b^2 - r^2) \\ &= z - 2ax - 2by + (a^2 + b^2 - r^2) \end{align*}$$ so this is the equation of the plane that cuts the paraboloid.

If $X'$ denotes the lifted copy of $X$, then it's not hard to see that:

• $D$ lies in $(ABC)$ iff $D'$ is below the plane $A'B'C'$
• $D$ lies outside $(ABC)$ iff $D'$ is above the plane $A'B'C'$

In other words, in the lifted picture, we would like a triangulation where each point is above the plane of any triangle. This is precisely the lower convex hull of the points!

There are technically some details left to check here, but I'm sure you now have a compelling mental picture of this.

Commentary. What's the closest we could have got to inventing this? There is another transformation one might think about that turns circles into planes: inverting about a point in space! If you redo this argument with inversion, you'll end up with the part of the convex hull that isn't visible from the center of inversion. You can think about how these are really "the same" argument.