SMO Senior 2025 ??% Speedrun

 (Glen here.)

The blog has been somewhat inactive because everyone has been busy, so sorry if we kept you waiting! I got sent this year's SMO Senior Round 2 paper this morning, so I thought I'd give it a shot. I don't have paper with me, so that's an extra challenge, I guess.

Problem 1

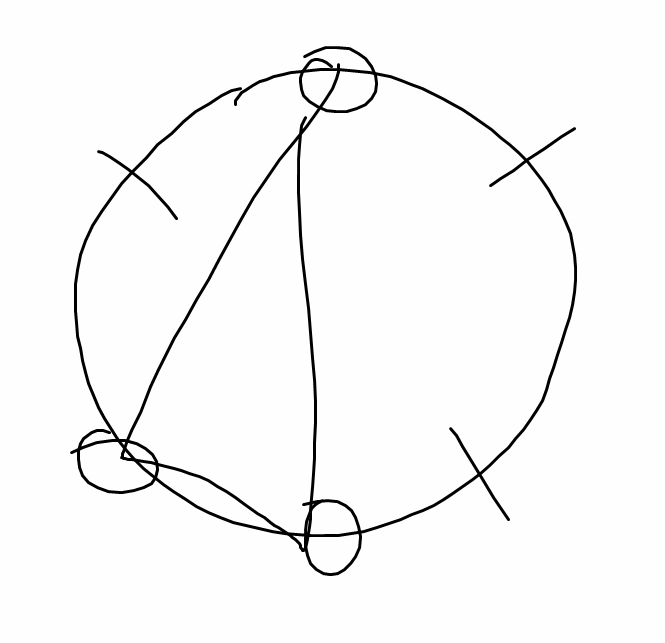
Let $ABCD$ be a convex quadrilateral and $M$ be the intersection of its diagonals. Through $M$ draw a line meetin [sic] the side $AB$ at $P$ sand [sic] the side $CD$ at $Q$. Find all the quadrilaterals so that there exists the segment $PQ$ that divides the triangles $ABM$ and $CDM$ into $4$ similar triangles.

• ??? What on earth is this???
• Here's a picture: 
  
• Ok, we probably need $\angle APM = \angle MPB = 90^\circ$? Yeah, if not, then each triangle has two distinct angles that add up to $180^\circ$, which is bad.
• This also tells us that $AB||DC$, as $PQ$ is perpendicular to both.
• If $\angle APM = 90^\circ$, then the only two possibilities for $APM$ and $BPM$ to be similar are if $MA=MB$ (so they are in fact reflections of each other), or $\angle AMB = 90^\circ$.
• Ah, if the first holds then we must also have $MC=MD$ because $AB||DC$ so $\triangle MAB \sim \triangle MCD$, and similarly if the second holds we must have $\angle CMD = 90^\circ$.
• So the only possibilities are: $ABCD$ is an isosceles trapezium with $AB||CD$, or $ABCD$ is a trapezium with $AB||CD$ and whose diagonals meet at an angle of $90^\circ$.

Time taken: 5 minutes

Problem 2

Let $I$ be the incentre of $\triangle ABC$ and $\omega$ be its incircle. Let $D$ be the intersection of $\omega$ with $BC$. Suppose $X,Y$ are points on $\omega$ such that lines $IX,IY$ and $AD$ are tangent to the circumcircle of $\triangle AXY$. Prove that line $XY$ bisects segment $BC$.

Proposed by Gabriel Goh

• Here's a really badly-drawn diagram:
  
• The $IX,IY$ tangent to $(AXY)$ is the same thing as saying that $(AXY)$ and the incircle are orthogonal to each other, i.e. inversion about the incircle sends $(AXY)$ to itself. So some sort of inversion/harmonic thing?
• How do we even draw this properly? Ok, inversion about the incentre sends $A$ to the midpoint of the $B$- and $C$-intouches, so it's the circle through that and $A$ that's tangent to $AD$ at $A$.
• Sigh, assuming I tried to bash this, I guess I could use complex numbers and put the incircle as the unit circle, but then $(AXY)$ would be yucky. It might be better to just go with coordinates...wait a second. I feel like I've done this before.
• Oh, turns out that I test-solved this about half a year ago. Apparently I tried to do some harmonic stuff and gave up and bashed. I really don't want to redo it, so here's what I sent Gabriel after solving it (minor edits to make the math more readable):

the bash is quite short but it took me quite a while to find a setup that doesn't explode

but the following turns out to be very doable:

• set $D(0,0)$, $A(0,1)$, $I(a,b)$, so $BC$ is $y = -\frac{a}b x$
• let centre of $(AXY)$ be $(x,1)$ and solve for $x$ using $OI^2 = ID^2 + AO^2$
• $XY$ is the difference of equations for $(AXY)$ and $\omega$
• solve for $XY$ intersect $BC$
• for tangents from $A$ to $\omega$, try to intersect $y = mx+1$ and $\omega$ to get a quadratic in $x$; this is a tangent line iff the quadratic in $x$ has a repeat root i.e discriminant $= 0$ (this is a quadratic in $m$). vieta gives sum & product of roots
• find $B, C$ in terms of $m$, then vieta to get $M$

under this setup nothing goes above a quadratic term i think

but there are a lot of similar setups which are significantly worse

for the record this gives $O\left(\frac{1-2b}{2a}, 1\right)$ and $M\left(-\frac{ab}{2a^2+2b^2-b}, \frac{a^2}{2a^2+2b^2-b}\right)$

I don't want to do this again but I do remember it being pretty short if you do it this way. I'm leaving it as an exercise if you want to practise your bashing. 

Time taken: ~ 1 hour (the first time I tried it)

Problem 3

Find all functions $f:\mathbb{Z}^+ \rightarrow \mathbb{Z}^+$, where $\mathbb{Z}^+$ is the set of all positive integers, such that for any positive integers $m,n$, $$f^{f(m)}(n)+n = f^m(n) + f(n).$$

 Proposed by Gabriel Goh

• Unfortunately, I have not test-solved this so I have to do it now.
• Why does this look so weird.
• I wonder if there's some way to think about it like that problem in Xu Chen's post.
• Intuitively, if $f$ makes things bigger, then this sort of makes sense: $f(n)$ beats $n$ but $f^{f(m)}(n)$ beats $f(n)$.
• If $f(m)$ beats $m$ by a lot, then $f^{f(m)}(n)$ might beat $f(n)$ by a lot, which might be bad since $f(n)$ beats $n$ by a fixed amount? Not really sure if this even makes sense.
• Let's try some actual cases. If $f(1)=1$, then putting $m=1$ gives $f(n)+n = f(n) + f(n)$ so $f(n)=n$ for all $n$. Cool.
• If $f(1)=2$, then $m=1$ gives $f(f(n)) + n = 2f(n)$. Put $n=1$, then we get $f(2)=4-1=3$. Ah, then we can induct to get $f(n)=n+1$.
• So maybe $f(n) = n+c$? Oh, this probably breaks for larger $c$. We have $n + cf(m) + n = 2n + cm + c^2$ on the LHS and $n + (m+1)c$ on the RHS so this only works if $c=0,1$, i.e. the two cases we considered.
• Let's try $f(1)=3$. Then $m=1$ gives $f(f(f(n))) + n = 2f(n)$. Put $n=1$, so $f(f(3)) = 6$. Uhhhh, $m=f(3)$ gives $f^6(n) + n = f^{f(3)}(n) + f(n) = f^3(n) + 2f(n) - n$...ok, that's not great.
• But maybe we could do some telescoping thing? Rearrange to get $f^{f(m)}(n) - f^m(n) = f(n) - n$. Then repeatedly replacing $m$ with $f(m)$, these telescope to give $f^{f^k(m)}(n) - f^m(n) =k( f(n) - n)$.
• A slightly better way of saying what I wrote just now is that if $f(m) > m$, then $f^{f(m)-m}(f^m(n)) - f^m(n) = f(n)-n$, so $f$ increases larger stuff slower, which is bad because everything's an integer.
• Of course, I'm implicitly assuming that we actually have $f(n) > n$ for all $n$. Can we prove this?
• Let's look again at $f^{f^k(m)}(n) - f^m(n) =k( f(n) - n)$. If $f(n) < n$ for some $n$, then the RHS is always $<0$, and in fact goes to $-\infty$ as $k$ goes to $\infty$. But that's bad, since we have $f^{f^k(m)}(n) =  f^m(n) + k( f(n) - n) > 0$.
• That's nice. What if $f(n) = n$ for some $n$? Then I guess putting $n$ in the equation does nothing. Oh, wait, but that means that $f^n(r) + r = f^n(r) + f(r)$ for each $r$, so $f(r)=r$ for all $r$.
• So we may indeed assume that $f(n)>n$ for each $n$. We probably just need to formalise this growth rate argument?
• Let $g(n) = f(n)-n$. Then we have $f^{g(m)}(f^m(n)) - f^m(n) = g(n)$. The LHS is at least $g(m)$, since each time we apply $f$, we're increasing by at least $1$. So this gives $g(n) \le g(m)$. But $m,n$ are arbitrary, so the reverse inequality holds and thus $g$ is constant. Ah, and that's the $f(n)=n+c$ case we checked above.
• Very cool problem!

Time taken: 30 minutes

Problem 4

Let $a_1,a_2,\ldots,a_n$ be positive numbers and $A$ their arithmetic mean. Prove that $$A^{n-1} \ge \frac1n\sum_{i=1}^n a_1\cdots \hat{a}_i\cdots a_n,$$ where $\hat{a}_i$ denotes the term $a_i$ is omitted.

• This hat notation is so algebraic topology-coded.
• Ok, this is a symmetric homogeneous $n$-variable inequality, and the RHS is $\frac1{n!}[1,1,\ldots,1,0]$.
• On the other hand, the left is $\frac1{n!}$ times a convex linear combination of stuff of the form $[a_1,a_2,\ldots,a_{n-1},0]$ where $a_1\ge \cdots \ge a_{n-1}$, but all of these majorise $[1,\ldots,1,0]$, so we're done by Muirhead.
• What?!

Time taken: 1 minute

Problem 5

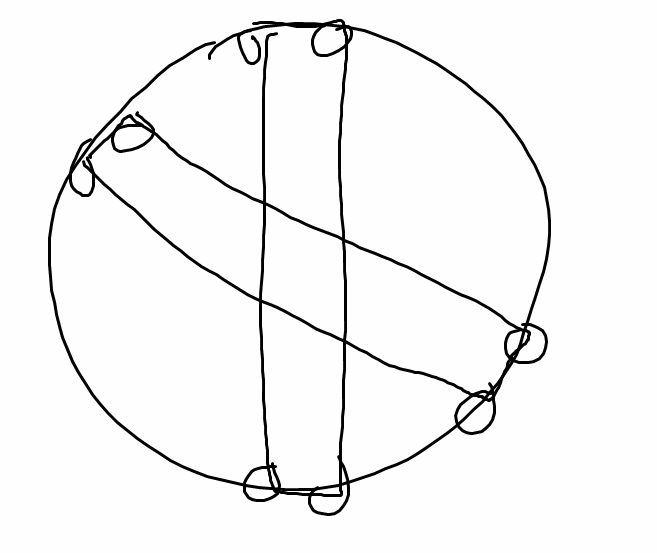
Find the smallest positive $m$ so that it is possible to choose $8$ vertices from a regular polygon with $m$ sides such that no three of them are the vertices of an isosceles triangle.

• Given one vertex $v$, for each other vertex $a$, for $v$ not to be the apex of an isosceles triangle, there must be some corresponding point $a'$ that's not chosen. So there are at least, like, $7$ holes? How well can these holes align when we vary $v$? Not sure but doesn't look like there are really any constraints.
• Let's try small cases. If $n=3$, we can only pick two vertices, duh. Same for $n=4$, and...uh...$n=5$ as well.
• For $n=6$, I think we can find a non-isosceles triangle:
  
• Oh, in fact we get an extra vertex for free:

  
• Hmm, I wonder if we have to use the fact that $8$ is a power of $2$. We could maybe try to generalise this by doing something like this?

  
• Let's try to actually make this work. Starting from the top and going anticlockwise, we have to skip one vertex between the two rectangles. And then, we have to skip like $4$ vertices?

  
• I think this works. There are $10$ blank vertices, so $18$ in total. We're actually helped a lot by the fact that a lot of the pairs can't be the base of an isosceles triangle, because there just isn't a vertex that's halfway between them. So the only things we have to check are these:

  
• Maybe we could use this to our advantage. I guess if there are an even number of vertices, we could colour them black and white alternatingly, and then if we choose a black and a white vertex, they can't be the base of an isosceles triangle. On the other hand, if we choose two things of the same colour, then there are two possible points that could make an isosceles triangle.
• Annoyingly, diametrically opposite points could be either the same or opposite colours, depending on whether $m$ is divisible by $4$.
• Anyway, suppose we have $4$ black (WLOG) vertices $A,B,C,D$ (arranged in this order). How many pairs of diametrically opposite vertices do they ban? That's the same as asking how many non-parallel lines we can draw from these vertices, and I think that's at least $4$ (two non-opposite sides and the two diagonals), so at least $8$ vertices banned in total.
• Well, I guess that tells us that if $m$ is even, then $m\ge 16$. Moreover, if $m=16$, all equalities must hold, and we must have $4$ black vertices and $4$ white vertices, each of which form a rectangle. Oh, I guess I also have to rule out $5$ black vertices $A,B,C,D,E$ (arranged in this order), but in that case we can look at, like, the five diagonals.
• Anyway, the rectangles can't be squares, since squares contain isosceles triangles. So they have to be as drawn below since that's the only way to get the vertices to be the same colour.

  
• But after we cross out the $8$ vertices these preclude, we're left with exactly a square, so that's not possible.

  
• We're left with the $m$ odd case but somehow I think that should be easier. Now, every chord can be the base of exactly one isosceles triangle, so we just want to find as many non-parallel chords that the cyclic octagon $ABCDEFGH$. I guess we can get $8$ by looking at everything that passes through $A$ plus $BH$, so there are at least $8$ blank vertices, which means (since $m$ is odd) $m \ge 17$. Sigh.
• Ok, we just have to rule out $m=17$. What now?
• This sort of reminds me of the Cauchy-Davenport theorem: given some residues $a_1,\ldots,a_8$ modulo $m$, we want to find how many values $a_i+a_j$ can take (or more accurately, $\frac{a_i+a_j}2$. But this only works if $m$ is prime...but wait! $m=17$ is prime.
• Aha, so by the Cauchy-Davenport theorem, there are at least $8+8-1 = 15$ values of the form $\frac{a_i+a_j}2$, so at least 15 unchosen vertices, contradiction.

Time taken: 1 hour

Post mortem

So that's about a total of just over 2.5 hours. That's longer than I thought it'd take me for an SMO Senior, oops. Thoughts about each of the problems:

Problem 1 is kind of silly. It's a matter of not getting thrown off by the scary $4$ similar triangles thing and just focusing on the pairs that are easy to compare.

Problem 2 is a lot harder than I'd expect for a SMO Senior Q2, but maybe I'm just bad at synthetic. I do remember having to play around with quite a few coordinate systems before settling on an approach that worked nicely. If you're looking to practise your bash, try other setups and see how they turn out! And of course, there's always my outline if you actually want to carry a bash out. I kind of like the Vieta trick: finding tangents is bad, but $M$ is symmetrically expressed in terms of the tangents, so we don't actually have to solve a quadratic.

Problem 3 is really cool. I like it.

Problem 4...I wonder if my solution would be accepted. In general, you're allowed to quote theorems unless they trivialise the problem, but also I technically have done a step of saying that upon expansion, every term on the LHS majorises the thing on the right? I bet there's some magic way to do this without overkilling with Muirhead, but an alternative approach is to go by induction and prove that $[1,0,\ldots,0][1,\ldots,1,0,\ldots,0] \ge [1,\ldots,1,1,0,\ldots,0]$ (the RHS has $k+1$ $1$s and the second term on the LHS has $k$). This reduces to showing that $[2,1,\ldots,1,0,\ldots,0] \ge [1,\ldots,1,1,0,\ldots,0]$ which should just be a sum of squares. But ew.

Problem 5: I wonder if this works for, say, general powers of $2$. I feel like my construction should generalise, and maybe we'd get $m=2\cdot 3^{a-1}$ if we want to choose $2^a$ vertices? Not sure. And I have no clue how we'd show the bound. I feel like I'm heavily exploiting the fact that the numbers are small, so we can just rule out all the cases by hand. This reminds me a lot of SMO Open 2016/5 which has a really slick double-counting solution which works for general positive integers, but Sheldon and I both abused the fact that the numbers were small and wrote out some horrible case-bash. On the other hand, this is the first time in my life that I used the Cauchy-Davenport theorem, so maybe that's cool, I guess.