More Rectangular Tilings
(This is Glen.)
Some time ago, Etienne posted about this problem on rectangle tilings, to which this was my reaction in our blog Discord channel:
I, too, think that this problem deserves an article of its own, and so this is my attempt.
Because the screenshot of the screenshot above is somewhat blurry, here's the statement:
A rectangle with sides $r$ and $1$ can be tiled with squares if and only if $r\in\mathbb{Q}$.
A large part of the reason why this is my favourite combi problem is because it has multiple very distinct proofs, each of which I find very cool. I'm familiar with three of these (and I am certain there are more): the most famous is by Max Dehn (of Dehn invariant fame) and can be found in Proofs from the Book (pages 195-196). I'm not going to go through the proof because it's very well-presented there, but I highly recommend looking at it. It involves viewing $\mathbb{R}$ as a vector space over $\mathbb{Q}$: this trick is also used in Dehn invariants and can be applied to solve actual Olympiad problems, for example this one that I dug up from some training set by Eugene:
Suppose $C = \{A_1, \ldots, A_{101}\}$ are cows. For each $i$, $C\setminus \{A_i\}$ can be partitioned into two parts of $50$ cows each such that the total weight of each half is equal. Show that all the cows have the same weight.
(Hint: this is a classical problem if you also insist that the cows have integer weight.)
Another proof is a one-liner using physics which I'll talk about at the end. The last one, and the one I'll focus on, is the proof I came up with when I first encountered this problem. (Well, actually that one had a small hole, and the patched version - which is what I'm presenting - is a little shorter.) It's (unsurprisingly) not as elegant as either of the others, but I think there is something to be said about it and general problem-solving metas.
Background
So, backstory. As a first-year undergrad, I had to do this introductory course called "Numbers and Sets", which is pretty trivial for anyone with a decent Olympiad background. The lecturer was, of course, aware of this, and so addition to the usual problem sheets, we also received some number of what he called "Introductory Problems". (Spoiler alert: they were not introductory.) If you solved enough of them, you'd unlock the next set, "More Introductory Problems", and if you solved enough of those, then you'd receive "Even More Introductory Problems". I am sort of curious what the next title would be, but I only got through about half of the last set. Anyway, this last set is where I first saw this problem on tiling rectangles, where it was phrased as:
Show that it is impossible to dissect a square into a finite number of rectangles, each of which has side-ratio $\sqrt{2}$.
At this point, you might be wondering how this is the same question. Well, suppose we've dissected a square into a finite number of rectangles with side ratio $\sqrt{2}$, then scale the whole diagram by $\sqrt{2}$ and you have a dissection of a $1:\sqrt{2}$ into a bunch of squares and dominoes (which you can just view as two squares), so we're done if we can prove the stronger problem statement. I actually like the $r=\sqrt{2}$ version of the problem more, because you can describe it very succinctly as "you can't cut a sheet of A4 paper into squares".
(Incidentally, tiling a $1:\sqrt{2}$ rectangle with squares is something Etienne tried to do in his initial investigations for his post, and this provides a very quick reason why it doesn't work without having to worry about how $\sqrt{2}$ looks like as a continued fraction.)
Anyway, I started thinking about this, drawing pictures and stuff, and then I began to realise that I had drawn some very similar pictures before...
The first step
So it turns out that drawing squares is hard because it's hard to guarantee that all four sides are equal. What I instead did was to draw a dissection of a rectangle into rectangles and ask "if these are all squares, what's the side ratio of the big rectangle?" You could then set all the side lengths of the rectangles to be variables, and with some amount of effort, solve for the possible side lengths that would make the diagram legal.
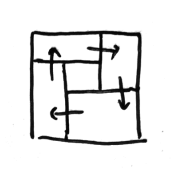
To be precise, whenever we see a pair of junctions as drawn below, the side lengths of the squares on either side add up to the same number:
(To deal with cross junctions, think of them as two T-junctions spaced infinitesimally apart, i.e. we "forget" that they are aligned.)
So we have a system of simultaneous linear equations. Trying some small cases, this is actually enough to force the side ratio of the big rectangle!
Here's an example:
Here's a slightly less silly example:
But what exactly do we know about these pairs of junctions? As it happens, a lot. Here's the problem I was thinking of as I was drawing these diagrams:
(ISL 2014 C1) Let $n$ points be given inside a rectangle $R$ such that no two of them lie on a line parallel to one of the sides of $R$. The rectangle $R$ is to be dissected into smaller rectangles with sides parallel to the sides of $R$ in such a way that none of these rectangles contains any of the given points in its interior. Prove that we have to dissect $R$ into at least $n+1$ smaller rectangles.
At first glance, this doesn't seem to be related at all (and in fact, when this problem appeared in NTST 2015, I ended up writing some horrible 5-page induction - sorry Yan Sheng). But in fact, a very quick double counting solution exists: count the number of pairs of T-junctions like the ones drawn above. More concretely, this is the key step in solving the question:
Lemma. In a dissection of a rectangle into $n$ smaller rectangles, there are $n-1$ T-junction pairs.
(As an exercise: 1) prove the lemma (hint: double count the number of right angles in the picture); 2) why does this solve 2014 C1?)
So applying this lemma, we have $n-1$ simultaneous equations to solve for $n$ side lengths. The extra degree of freedom comes from the fact that you can scale the whole diagram. Now, all we need to prove is that these equations are linearly independent!
The next step
We now have a system of $n-1$ linear equations in $n$ variables, each of form $x_{a_1} + \cdots + x_{a_k} = x_{b_1} + \cdots + x_{b_l}$. Suppose they are linearly dependent, so we can scale some of these equations and add them up to get $0=0$. Graphically, we can view this as an arrow pointing from the "positive side" to the "negative side":
Looking at each of the inner square individually, they either have no arrows pointing in/out of them, or both in- and out-arrows. To look for a contradiction, it would make sense to show some square only has arrows pointing into it or out of it.
Let's try to draw a counterexample and see how we fail. Something like this looks reasonable, until you realise this forces the inner square to only have out-arrows:
In a way, the "bad" square seems to be identifiable since the arrows swirl around it. This reminded me of yet another question about rectangle dissections:
(ISL 2007 C2) A unit square is dissected into $n>1$ rectangles such that their sides are parallel to the sides of the square. Any line, parallel to a side of the square and intersecting its interior, also intersects the interior of some rectangle. Prove that in this dissection, there exists a rectangle having no point on the boundary of the square.
Here's a proof without words (courtesy of AoPS):
(Interestingly, the official ISL booklet has two solutions, neither of which is this.)
Of course, in our setup, arrows point transversely to edges, but we can easily rectify that by rotating all arrows anticlockwise by $90$ degrees. In our picture above, the boundary of the inner square now becomes an anticlockwise loop. Note that for a contradiction, we don't even need all the edges to be directed; we just need at least one edge to be directed and for all the directed edges to agree.
Now, we would like to say "just keep walking along edges until we enter a loop", but there are several problems, for starters:
- Some edges don't have a direction (not every equation has to be used in our linear combination). Maybe we could just pick a direction for all of them?
- What happens if the loop we end up in consists only of (previously) undirected edges?
- What if the loop contains multiple squares?
So there is still some work to be done. But as it turns out, these issues are not hard to resolve.
Finishing up
Let's look back at the original version of arrows, which point from squares to squares. Starting from a square with an out-arrow, we can travel to another square along an out-arrow, and since all squares with an in-arrow also have an out-arrow, we can repeat this process. Now, the choice of out-arrow isn't unique, but we could force a choice: upon entering a square, we travel clockwise along the boundary until we first meet an edge we can exit by.
It's not hard to see that this agrees with the direction of an edge, when that exists. Moreover, travelling now depends only on which square you're in and which edge you're on, so we eventually enter a cycle. Note that this cycle is not self-intersecting (to resolve the case where we travel in both directions on an undirected edge, we view the path drawn as being slightly in the interior of the squares, and only crossing directed edges).
(We have now resolved the first bullet point. We also always travel in rectangles with arrows, which in a way resolves the second.)
Hence, this cycle we've constructed bounds some region $R$ in the rectangle. Our main problem now is to resolve the last bullet point, i.e. "shrink" $R$ to some inner rectangle.
Before we proceed, note that directed edges are the only edges we can cross, and there are only two ways to do so, by the "exit by first possible edge" rule:
In fact, the diagram on the right is the only way we can turn left, and the only way we can turn right is when we can't cross an edge when we reach the corner of a squares.
Also note that the cycle can't just be stuck in one square, since we must exit every square we enter.
Now, we consider two cases.
Case 1: The cycle goes clockwise around $R$ (when travelling along the cycle, $R$ is always to the right).
Note that in this case, our cycle is slightly within the boundary of $R$.
The only arrows (if any) on the boundary point from outside $R$ to inside $R$. Consider doing the same process as above starting from some square in $R$ (well, on the boundary of $R$, so said square has an out-arrow), but instead of travelling clockwise around a square's boundary by default, we travel anticlockwise instead. (For this to work with our direction conventions, we need edge directions to arise from the arrows rotated $90$ degrees clockwise instead of anticlockwise. An easy way to fix this is to consider the mirror image.)
The new limiting cycle is stuck inside $R$. Moreover, it's strictly smaller: for equality, we'd have to trace the boundary (along the inside) in the opposite direction, which would mean crossing directed edges in the opposite direction from before.
Case 2: The cycle goes anticlockwise around $R$ (when travelling along the cycle, $R$ is always to the left).
In this case, the cycle is slightly outside the boundary of $R$.
Here, the only arrows on the boundary point from inside $R$ to outside of $R$. Notice that I've omitted the "if any": in this case, we must turn left at some point, at which point we are travelling along a directed edge.
Now reverse all arrows (i.e. swap all the sides of our linear equations) and repeat the process, starting from some square inside $R$. Since all arrows on the boundary now point into $R$, we can't exit $R$. Hence, we now get another cycle which is contained in $R$.
The new bounded region is always strictly smaller than $R$, unless we end up travelling clockwise around the boundary of $R$ (i.e. Case 1). On the other hand, when we resolve Case 1, we always end up with a strictly smaller region.
Repeating, we can reduce $R$ to a single square. As mentioned above, we can't be stuck inside the square, which means that we must be in Case 2, i.e. the square has at least one directed edge pointing outwards. But then when adding up our linear equations, the corresponding variable has a positive coefficient, contradiction.
And at long last, we are done!
Meta-commentary for young people
Having read my solution, my supervisor's only remark was "How did you know this would work?" And I can see where he's coming from: there are a whole bunch of unrelated ideas which don't seem to directly help. But in a way, this was the most natural thing for me to do: I had seen every trick in this proof before.
Indeed, I'm certain I would never have found this proof if I hadn't known the fact about the number of junction-pairs, had I been content with my (long) induction solution back in the day and not bothered to learn the intended solution. (Though really, the main reason why this stuck in my mind was because I had tried quite hard to double count during NTST but failed because I was not double counting the right quantity.) Neither would I have found the proof had I not seen the "walk until you enter a cycle" idea before (or if I'd found one of the two official solutions and not bothered to look up the one-liner).
So I guess my point is: learn (alternate, better) proofs even if you've seen one way to solve a question. (This applies to this problem as well! There are three separate proofs in this post, each with something different to offer.)
Meta-commentary for old people
Uh, digression.
For the cow problem above, there's one linear algebra solution which I'm alluding to above which boils down to "works over $\mathbb{Z}$ $\Rightarrow$ works over $\mathbb{Q}$ $\Rightarrow$ works over $\mathbb{Q}^n$", but there's also another solution in which you encode the question conditions in terms of $101$ simultaneous equations, show that the rank of the resulting matrix is $100$, and hence we have a one-dimensional solution space given by all cows having the same weight.
Compare that to this problem. We have Dehn's proof by considering a suitable $\mathbb{Q}^n$, and this other one in which you show the solution space of some system of linear equations is one-dimensional.
There's probably some nice duality (in the sense of vector spaces) reasoning behind this, but I haven't really thought much about it.
Epilogue
So why is this my favourite combi problem? I had already found it pretty cool that I could solve this question on rectangle dissections by applying two other questions on rectangle dissections I had seen. As it turned out, my supervision partner had found yet another solution, some analytic approach to do with approximating the side lengths by rational numbers. I found out about Dehn's brilliant proof later. But the kicker was this: our supervisor showed us this one-line proof using physics:
Convert the diagram into a network of resistors:
Then we're left with proving that a finite network of rational resistors has rational resistance, which is true by repeatedly applying $Y-\Delta$.
(Surprisingly, this idea also appears in other places: see Conway's classification of rational tangles.)
I would, I think, be hard-pressed to name a combi problem as varied in solutions as this one.














Comments
Post a Comment