Visualising FEs!

 (Drew here.)

Three weeks ago, we had a post about visualising combi, and last week, it was about the anatomy of an FE. Out of sheer coincidence, here I am now talking about visualising FEs! A nice way to avoid the notoriously grindy nature of FEs and favour a combi main like me :)

Let's begin with a familiar one: Cauchy's functional equation.

(Positive real Cauchy) Find all $f:\mathbb R^+\to\mathbb R^+$ satisfying $f(x+y)=f(x)+f(y)$ for all $x,y\in\mathbb R^+$.

The solutions to this are $f(x)=cx$ for $c\in\mathbb R^+$, which are all linear functions.

For any integer $n$, we can calculate

$$\begin{align*}f(nx)&=f((n-1)x+x)\\&=f((n-1)x)+f(x)\\&=f((n-2)x)+f(x)+f(x)\\&=\dots\\&=\underbrace{f(x)+f(x)+\dots+f(x)}_n\\&=nf(x).\end{align*}$$

So given a rational number $r=\frac mn$ we have that \[f(rx)=f\left(\frac mnx\right)=mf\left(\frac xn\right)=\frac mnf\left(\frac xn\cdot n\right)=\frac mnf(x)=rf(x).\]

Now back to the main topic, let's graph this function.

Suppose $f(1)=c_1$ for some $c_1$, then $f(r)=c_1r$ for all rational $r$, which forms a (dotted) line.

What if $f(t)=c_2$ for some other $c_2\neq c_1$? We get two different lines on the graph.

Could the graph of $f$ have two lines like this?

Let's not forget that we are working over $\mathbb R^+$ over here, so we can get inequalities like $f(x+y)-f(x)=f(y)>0$, or in other words $f$ is increasing. Pictorially, this means any point $(x,f(x))$ "bans" a rectangular region below or above it, those which would connect to form negative gradient.

However, any other line must intersect this banned region (check that there exists a rational number $r$ such that $(r,c_2r)$ lies in the region), so in fact it's impossible to have $c_2\neq c_1$. We conclude that $f(x)=c_1x$ for all $x$.

Black "banned" region intersects every other line.

Let's take closer look at what this solution uses:

1. It creates a lot of points from one "seed". In this case, all the rational multiples of $x$ have their values known. Later we will see more complicated things that seeds can generate!
2. Inequalities are used to create a "banned region". This is quite important to determine the shape of the graph.

In fact, with (2), we can look at another solution to finish the above: consider the union of banned regions generated by every point $(r,f(r))$!

The banned regions sweep out the entire quarter-plane, leaving only the points on the line $c_1x$ unbanned. (Again, one must write up the details of this slightly more carefully.)

No line may pass!

Moving on to the next example:

(MOP '24 HW) Find all $f:\mathbb R\to\mathbb R$ satisfying $f(x^2)=f(x)^2$ and $f(x+1)=f(x)+1$ for all real numbers $x$.

The solution we're looking for here is $f(x)=x$.

First, let's eliminate some banned region: $f(x)=f\big(\sqrt x\big)^2\geq0$ for all $x\geq0$, banning the 4th quadrant.

Then, using the second condition we can translate any seed point $(x,f(x))$ to $(x+n,f(x)+n)$ for any integer $n$, and this may not land in the banned region either.

"Banned" staircase region.

Now there seems to be this empty region below the line $y=x$, so let's settle that. Shift to a seed point $(s,f(s))$ where $1<s<2$ and repeatedly apply the first operation with $x=s$, $x=s^2$ etc.

This creates a number of points lying on the curve $y=x^{\log_s{f(s)}}$ (verify this!), where the exponent is less than 1. But the $x$ coordinate is unbounded, while the curve eventually nestles in the banned region, so this is impossible.

They trespass into the forbidden region!

The upper half of the first quadrant is now easily handled by finding a corresponding negative point that lies under the line $y=x$.

Flip it downstairs! Or maybe downhill, since the stairs are gone now.

So $f(x)=x$ for all $x>0$, and translation with the second condition gives the only solution $f(x)=x$.

(For the record, this solution allowed me to headsolve the problem in the plane! Also, this has been called a "homophonic" FE, because the LHS and RHS both sound the same when read out, making it nontrivial to communicate the statement.)

Again, the two things are present: the seed points and banned regions have great synergy with each other.

Finally, let's conclude with a problem from the USAMO last year:

(USAMO 2023/2) Find all functions $f:\mathbb R^+\to\mathbb R^+$ satisfying $f(xy+f(x))=xf(y)+2$ for all $x,y\in\mathbb R^+$.

 We begin with some classic FE techniques:

• The solution is $f(x)=x+1$ only.
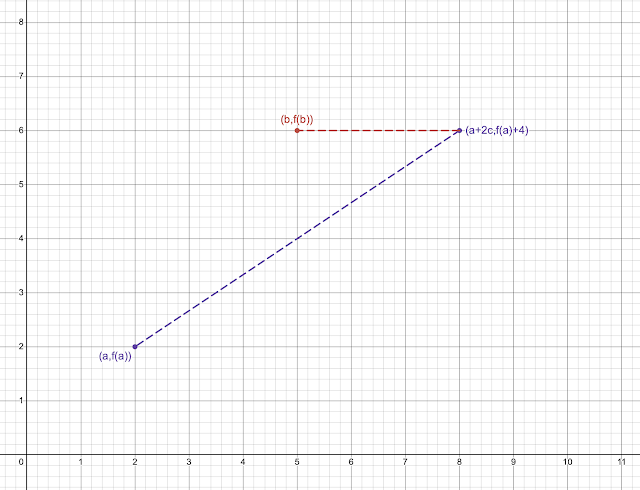
• By substituting $x=1$, we get $f(y+c)=f(y)+2$ where $c=f(1)$.
• For injectivity, if $f(a)=f(b)$, then $$af(b)+2=f(ab+f(a))=f(ab+f(b))=bf(a)+2=bf(b)+2$$ so $a=b$.
• We can also prove surjectivity to $(2,\infty)$, by making the substitution $x=\frac{t-2}{c}$ and $y=1$, making $t=f(...)$ for any $t>2$.

Question: what if $f(a)\equiv f(b)\pmod 2$?

If $f(a)+2n=f(b)$, then $f(a+cn)=f(b)$ so $a+cn=b$ by injectivity.

Dare defy injectivity?

With this in mind, $f(x)>4$, then $f(x-c)=f(x)-2=f(r)$ for some $r$ by surjectivity, and $r=x-c$ by injectivity. Thus $x>c$.

Equivalently, $f(x)\leq4$ whenever $x\leq c$. Surprise, we've got banned region again!

The black region is banned; the graph of $f$ must stay in the highlighted region on the interval $(0,c]$.

And now we can translate this highlighted region using the condition $f(y+c)=f(y)+2$. Zooming out, we get the following graph:

Starting to look linear?

Formally, we can show that $\frac2cx-2\leq f(x)\leq\frac2cx+4$. In other words, the graph is bounded by the two red lines in the diagram above.

So, we can now make the substitution $(x,x)$ to get $f(x+f(x))=xc+2$. But the LHS is approximately $\frac2cx+\frac4{c^2}x$, off by at most a constant. Therefore $\frac2c+\frac4{c^2}=c$, otherwise the difference between the $x$ terms on the LHS and RHS can grow arbitrarily large!

Solving the cubic gives $c=2$ as the only real solution, and from here it's not hard to finish with the knowledge of $f(1)=2$.

This problem had a slightly different flavour to it, with more focus on actually doing standard stuff + calculations. But the translations (point 1) / boundedness (point 2) / linearity are still readily visualised on the graph!

I really enjoy coming up with solutions like these, because they're less heavy on "FE trickery" and run-of-the-mill techniques, and showcase a unique perspective in FEs! Some other problems that feature graphical ideas / solutions are USAMO 2000/1, IMO 2013/5, and USA TST 2021/3, so if you reallyloveFEs, go try them out!

(Oh, and here's the Desmos link!)